【整理】算法竞赛字符科技学习笔记
|
|
2
|
算法
|
435

3732 字
|
39 分钟

内容参考：

牛客竞赛字符串专题-calabash_boy
樱雪喵-广义后缀自动机（广义 SAM）学习笔记

KMP

KMP 是一种用于两个字符串匹配的算法。其核心概念是 Border ，即一个字符串同长度的完全相同的前后缀（通常不含自身）。

KMP 的做法是先求出要匹配的字符串（短串）的所有前缀的最长 Border，然后在于长串进行匹配，并在无法匹配时跳转到其 Border 进行再次尝试匹配。详细方法可以参考我之前的学习笔记。

有时也会用 $next_i$ 表示字符串 $S$ 的前缀 $Preffix_i$ 的非平凡的最大 Border。

时间复杂度为 $O(n)$。

扩展 KMP (exKMP/Z 函数)

扩展 KMP 可以求两种东西：

  1. 一个字符串 $S$ 的每一个后缀与自己的 LCP
  2. 一个字符串 $S$ 的每一个后缀与另一个字符串 $T$ 的 LCP

做法是不断延申能够匹配到的最远位置，然后根据最远位置 $p$ 去找当前位置已经被匹配的长度。若超过 $p$ 则暴力匹配，否则直接得到当前位置的答案，显然 $p$ 的增长次数和暴力匹配的次数同级，故时间复杂度为 $O(n)$.

Hash

字符串 Hash 就是指将一个字符串映射成一个整数值的方法，通常用来快速比较两个字符串是否相等。

多项式取模 Hash(模哈) 时一个常用的哈希方法，即将字符串转换为 26 进制（或其他进制）数后进行取模，为了减少哈希冲突的可能性，双模是一个更优秀的选择。

双模（多模）：进行多次不同质数的单模哈希，有效降低冲突概率。在不泄露模数的前提下，没有已知方法可以构造冲突。

Trie 树

Trie 是一棵有根树，每个点至多有 $|\Sigma|$ 个后继边（即字符的可能种类数），每条边上有一个字符。每个点表示一个前缀：从跟到这个点的边上的字符顺次连接形成的字符串。
每个点还有一个终止标记：是否这个点代表的字符串是一个字典串（可以用 $match$ 数组将字典串映射到字典树上）。详细方法可以参考我之前的学习笔记。

时间复杂度为 $O(n)$。

Border 树

对于一个字符串 $S，n = |S|$，它的 Border 树（也叫 next 树）共有 $n + 1$个节点：$0, 1, 2, \dots, n$。
$0$ 是这棵有向树的根。对于其他每个点 $1 ≤ i ≤ n$，父节点为 $next[i]$。

$next[i]$ 表示字符串 $S$ 的前缀 $Preffix[i]$ 的非平凡的最大 Border。

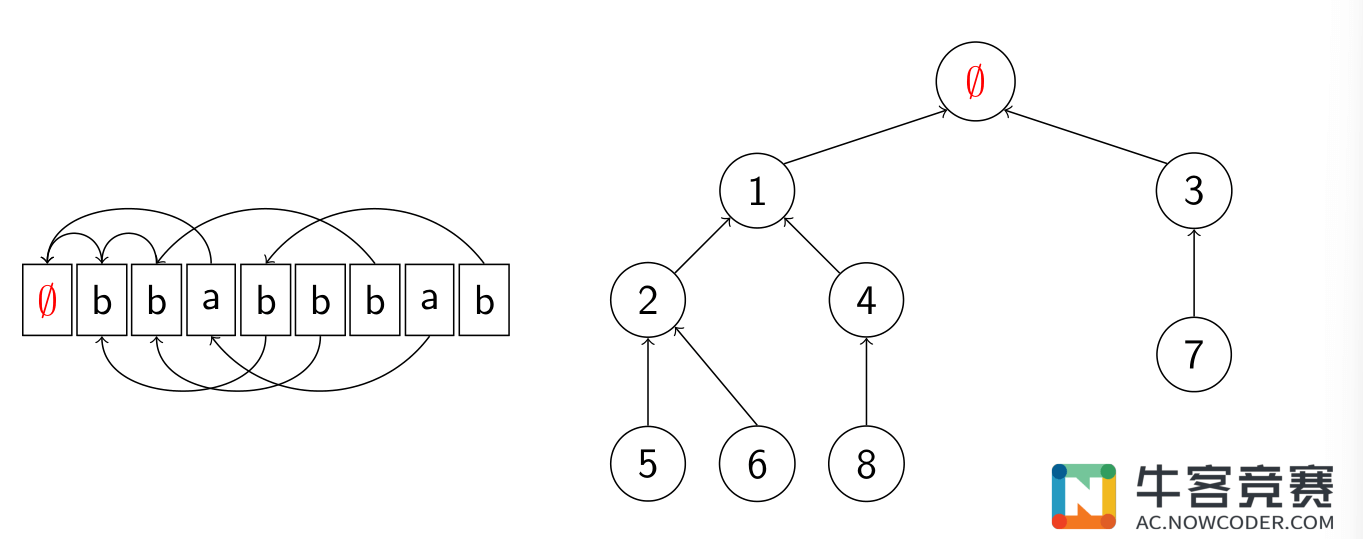
image-20240624141510116

上图就是一颗 Border 树（图源：牛客竞赛）

关键性质：

  • 每个前缀 $Prefix[i]$ 的所有 Border：节点 $i$ 到根的链。
  • 哪些前缀有长度为 $x$ 的 Border：$x$ 的子树。
  • 求两个前缀的公共 Border 等价于求 LCA。

例题：

AC 自动机（ACAM）

AC 自动机是 Trie 和 KMP 的结合，其构建分为以下两步：

  1. 构建 Trie 树。
  2. 构建 Fail 指针（失配指针）。

失配（Fail）指针： 对于 Trie 中的每一个节点（即某个字典串的前缀），它与 Trie 中所有串的最大 Border 即为失配指针。（这里的 Border 指的是广义 Border）

广义 Border：对于串 $S$ 和一个字典 $D$，相等的 $p$ 长度的 $S$ 的后缀，和任意一个字典串 $T$ 的前缀称为一个 Border。

如何进行查询？也分为两步：

  1. 在 Trie 树上依次遍历整个文本串（通过构建 Fail 指针时构建的通道在树上跳转），并给遍历的点都打上标记（加上权值，表示遍历了以该点为结尾的字符串）
  2. 对于通过 Fail 指针构成的图进行拓扑排序，把对应点的贡献也算入到 Fail 指针指向的点。

详细方法可以参考我之前的学习笔记。

时间复杂度为 $O(n)$。

Manacher

Manacher 可以求出一个字符串中以每个点为中心的最大回文串长度。

Manacher 算法的步骤如下：

  1. 记录最右回文串的中心 $mid$ 和左右端点 $L,R$（最右回文串：所有已求得的回文串中，右端点最靠右的一个）。
  2. 假设我们已经求出了 $1,2,\dots,i-1$ 位置的 $Len$（即以该位置为中心的最长回文串长度），则对于 $Len[i]$：
    1. 若 $i > R$：暴力拓展，并更新最右回文串。
    2. 若 $i \le R$：找到 $i$ 关于 $mid$ 的对称位置 $j=2\times mid -i$。
      1. 若 $j − Len[j] + 1 > L$，即 $Len[j]$ 没有超过当前最右回文串的表示范围，直接令 $Len[i]=Len[j]$ 即可。
      2. 否则，令 $Len[i]=Len[j]$，然后再暴力拓展，并更新最右回文串。

PAM（回文自动机）

PAM 是一种能够识别所有回文子串的数据结构。

关键概念：

  • 节点：每个节点代表了一种回文串。结点的 $len$ 属性即为其对应的回文串长度。
  • 后继边：用 $trans(u, ch) = v$ 表示 $u$ 节点有后继边 $ch$ 指向 $v$ 节点。则有 $S(v) = chS(u)ch$，以及
    $len[v] = len[u] + 2$.
  • 失配边：每个节点都有一个失配边，用 $fail[u] = v$ 表示 $u$ 节点的失配边指向了 $v$ 节点。则有 $S(v)$ 是 $S(u)$ 的最大 $Border$，即最长回文后缀。

PAM 的构造方法的核心即为 $fail$ 的构造方法。我们通过枚举前一个位置的 $fail$ 并依次跳转 $fail$，判断是否合法来进行构造，其部分代码如下：

int get_fail(int v,int p){
    while(p-tr[v].len-1<0||s[p-tr[v].len-1]!=s[p]){
        v=tr[v].fail;
    }
    return v;
}

注意，PAM 有两个根结点，一个为奇长度根节点，长度为 $-1$，一个为偶长度根节点，长度为 $0$，且 $fail$ 互相指向。

在 insert 一个字符时，我们先找到父节点的 $fail$，然后将这个字符连接到该节点的后面。然后更新该结点的 $fail$ 为其父节点的 $fail$ 结点与该字符继续进行 $get_fail$ 的操作。

SA（后缀数组）

关键数组：

  • $sa[i]$： 排名为 $i$ 的后缀是以第 $sa[i]$ 字符开始的后缀
  • $rk[i]$： 以第 $sa[i]$ 字符开始的后缀的排名
  • $height[i]$： 后缀 $i$ 与排名在他前面一个的后缀的 LCP(longest common prefix，最长公共前缀)
  • $H[i]$： 排名为 $i$ 与 $i − 1$ 的串的 LCP

求 SA：

  1. 假设当前已经得到了 $S(i, k)$ 的排序结果，即 $rk[S(i, k)]$ 与 $sa[S(i, k)]$，那么比较 $S(i, k + 1)$ 与 $S(j, k + 1)$ 字典序可以转化为先比较 $S(i, k)$ 与 $S(j, k)$，再比较 $S(i + 2k, k)
    $ 与 $S(j + 2k, k)$。
  2. 因此可以将 $S(i, k + 1)$ 看作一个两位数，高位是 $rk[S(i, k)]$，低位是
    $rk[S(i + 2k, k)]$。
  3. 用基数排序解决。

由于基数排序时间复杂度为 $O(n)$，总共要排 $O(\log n)$ 次。故时间复杂度为 $O(n\log n)$，需要注意的是，该算法常数较大。

通过 DC3 法 或 SA-IS 法，可以在 $O(n)$ 时间复杂度内求出 SA，但较为复杂，此处暂且按下不表。

求 Height：

  • 性质 $1$：设有一组排序过的字符串 $A = [A_1, A_2, \dots, A_n]$​，则有 对于任意的 $k \in [i, j]$，$LCP(A_i, A_j) =
    LCP(LCP(A_i, A_k), LCP(A_k, A_j)) = min(LCP(A_i, A_k), LCP(A_k, A_j))$​。进而，$LCP(A_i, A_j) = min(LCP(A_i, A_{i+1}), LCP(A_{i+1}, A_{i+2}), \dots , LCP(A_{j−1}, A_j))$。
  • 性质 2：$height[i] ≥ height[i − 1] − 1$。

由性质 2，我们发现我们可以暴力求 $height$（维护一下某个 $k$，当 $i$ 增加时 $k$ 减 $1$，然后直接从长度 $k$ 开始比较就行了），根据势能分析，时间复杂度为 $O(n)$。

实际应用中，使用 $H$ 数组更多一些。

SAM（后缀自动机）

后缀自动机是一种自动机。SAM 上的某个结点都表示若干个子串，这些子串的特点是他们在原字符串上所有出现位置的右端点都相同。

对于每一个结点（状态）有三种属性，$to[u][ch]$ 表示状态 $u$ 添加上 $ch$ 字符所到达的状态；$fa[u]$ 或 $lnk[u]$ 表示 SAM 上树边的父亲节点（后缀链接树），$l[u]$ 表示状态 $u$ 所能表示的最长子串的长度。

还有一些不会被记录的概念和性质：

  • $Right[u]$ 表示状态 $u$ 所表示的所有子串的出现位置的右端点集合。两个不同状态的 $Right$ 集合必然是不同的。
  • 任意串 $w$ 的后缀全部位于 $s(w)$（即 $w$ 对应的状态）的后缀链接路径上（即该点到根节点的路径上）。

SAM 的构建方法比较复杂，可以参考下述代码：

void add(int c){
    int p=last,np=++tot;//建新点 np
    // for(int i=0;i<26;i++) to[np][i]=0;
    l[np]=l[p]+1;last=np;cnt[np]=1;//更新相关属性
    while(p!=-1&&!to[p][c]){//从 p 点往上走到第一个 to[p][c] 不为空的点
        to[p][c]=np;//过程中所有点都向 np 连边
        p=fa[p];
    }
    if(p==-1) fa[np]=0;//如果一路到根，直接结束
    else{
        int q=to[p][c];//否则，考虑第一个已有的 q=to[p][c]
        if(l[q]==l[p]+1) fa[np]=q;//如果 l[q]==l[p]+1，直接链接父亲
        else{
            int nq=++tot;//否则，将 q 分为 nq 和 q 两个结点
            l[nq]=l[p]+1;
            for(int i=0;i<26;i++) to[nq][i]=to[q][i];
            fa[nq]=fa[q];fa[np]=fa[q]=nq;//更新相关属性
            while(p!=-1&&to[p][c]==q){//将 p 到根的路径上所有连向 q 的点都改为连向 nq
                to[p][c]=nq;
                p=fa[p];
            }
        }
    }
}

在构建完 SAM 后，很多题目需要在 Link 树上进行拓扑排序来更新答案，可以对所有状态根据 $l[s]$ 进行基数排序（桶排）来更新，代码如下：

vector<int> vec[N];
void topu(){
    for(int i=1;i<=tot;i++) vec[l[i]].pb(i);
    for(int i=s.length();i>=1;i--){
        for(auto u:vec[i]){
            cnt[fa[u]]+=cnt[u];
        }
    }
}

广义 SAM

广义 SAM 就是对多个字符串建立出一个 SAM，或对一棵 Trie 树建立 SAM.

首先，先对单串 SAM 上的定义进行拓展，本部分引用自 樱雪喵-广义后缀自动机（广义 SAM）学习笔记

  • 后缀

首先定义 Trie 树为 $S$, $S_{x,y}$ 表示 Trie 上从点$x$到点$y$的路径组成的字符串。
那么它的所有后缀可以表示为 ${S_{x,y}\mid y\in \text{subtree}(x),\text{y is leaf}}.$
广义 SAM 压缩的就是该集合内的后缀。

  • endpos 集合 （即本人笔记中的 Right 集合）

更改了后缀的定义，一个字符串 endpos 集合的定义也随之改变：$\mathrm{endpos}(t)={y\mid y\in\mathrm{subtree}(x),S_{x,y}=t}。$

  • 后缀链接 link

在新的 endpos 定义下，可以沿用后缀链接 link 的原定义。

那么我们根据新的定义对 Trie 构建出的 SAM 结构，就可以称作广义 SAM。

广义 SAM 的构建有离线和在线两种方法，离线做法是在 Trie 树上进行 bfs，然后 add 一个点时将 last 设置为在 Trie 树上父亲所对应的 SAM 上的点即可，事件复杂度为 $O(n)$，其中 $n$ 为 Trie 上的点数。

在线做法则需要对 add 函数进行一些修正以使其不建出空节点来，修正后不需要再建 Trie 树，事件复杂度为 $O(m)$，其中 $m$ 为字符串的长度和。

杂记

  • LCP（最长公共前缀） 可以通过二分 Hash 在 $\log(n)$ 的复杂度内完成（前提是 Hash 可以预处理）。

代码

KMP

void kmp(string a,string b){//a 为原串（长），b 为需要被匹配的串（短）
    int la=a.length(),lb=b.length();
    int j=0;
    for(int i=1;i<lb;i++){
        while(j&&b[i]!=b[j]) j=border[j];
        if(b[i]==b[j]) j++;
        border[i+1]=j; 
    }
    j=0;
    for(int i=0;i<la;i++){
        while(j&&b[j]!=a[i]) j=border[j];
        if(b[j]==a[i]) j++;
        if(j==lb){
            //printf("%d\n",i-lb+1); 这是 b 在 a 中出现的位置，从 0 开始
            j=border[j];
        }
    }
}

exKMP

void get_nxt(const string& s){//求 s 的所有后缀和 s 的 LCP
    int k=1,p=0,n=s.length();
    nxt[0]=n;
    while(p+1<n && s[p]==s[p+1]) p++;
    nxt[1]=p;
    for(int i=1;i<n;i++){
        if(i+nxt[i-k]<=p) nxt[i]=nxt[i-k];
        else{
            int j=max(0,p-i+1);
            while(i+j<n && s[i+j]==s[j]) j++;
            nxt[i]=j;p=i+nxt[i]-1;k=i;
        }
    }
}
void get_ext(const string& s,const string& t){//求 s 的所有后缀和 t 的 LCP
    int na=s.length(),nb=t.length();
    int p=0,k=0;
    while(p<na && p<nb && s[p]==t[p]) p++;
    ext[0]=p;p=ext[0]-1;
    for(int i=1;i<na;i++){
        if(i+nxt[i-k]<=p) ext[i]=nxt[i-k];
        else{
            int j=max(0,p-i+1);
            while(i+j<na && j < nb && s[i+j]==t[j]) j++;
            ext[i]=j;p=i+ext[i]-1;k=i;
        }
    }
}

AC 自动机（ACAM，含 Trie）

struct ACAM{
    struct Trie_Tree{
        int fail,to[26],ans;
    }tr[N];
    int match[N],tot,in[N];
    inline void insert(string s,int k){
        int l=s.length();
        int u=0;
        for(int i=0;i<l;i++){
            if(!tr[u].to[s[i]-'a']){
                tr[u].to[s[i]-'a']=++tot;
            }
            u=tr[u].to[s[i]-'a'];
        }
        match[k]=u;
    }
    inline void Get_Fail(){
        queue<int> q;
        for(int i=0;i<26;i++)
            if(tr[0].to[i]) q.push(tr[0].to[i]);
        while(!q.empty()){
            int u=q.front();q.pop();
            for(int i=0;i<26;i++){
                if(tr[u].to[i]){
                    tr[tr[u].to[i]].fail=tr[tr[u].fail].to[i];
                    in[tr[tr[u].to[i]].fail]++;
                    q.push(tr[u].to[i]);
                }
                else tr[u].to[i]=tr[tr[u].fail].to[i];
            }
        }
    }
    inline void query(string s){
        int l=s.length();
        int u=0;
        for(int i=0;i<l;i++){
            u=tr[u].to[s[i]-'a'];
            tr[u].ans++;
        }
    }
    inline void topu(){
        queue<int> q;
        for(int i=0;i<=tot;i++) if(in[i]==0) q.push(i);
        while(!q.empty()){
            int u=q.front();q.pop();
            in[tr[u].fail]--;
            tr[tr[u].fail].ans+=tr[u].ans;
            if(!in[tr[u].fail]) q.push(tr[u].fail);
        }
    }    
}AC;

Manacher

string init(string t){
    string tmp;
    tmp+="#";
    for(auto ch:t){
        tmp+=ch;
        tmp+="#";
    }
    return tmp;
}
int p[N];
void manachar(){
    int L=-1,R=-1,mid=-1;
    for(int i=0;i<s.length();i++){
        if(i>R){
            mid=i;R=i;L=i;
            while(R+1<s.length()&&L-1>=0&&s[R+1]==s[L-1]){
                R++;L--;
            }
            p[i]=R-mid+1;
        }
        else{
            int j=2*mid-i;
            if(j-p[j]+1>L){
                p[i]=p[j];
            }
            else{
                mid=i;L=2*i-R;
                while(R+1<s.length()&&L-1>=0&&s[R+1]==s[L-1]){
                    R++;L--;
                }
                p[i]=R-mid+1;
            }
        }
    }
}

PAM

string s;
struct PAM{
    int u=0,tot=1;
    struct node{
        int to[26],fail,cnt,len;
    }tr[N];
    void init(){
        tr[0].len=0;tr[1].len=-1;
        tr[0].fail=1;tr[1].fail=0;
    }
    int get_fail(int v,int p){
        while(p-tr[v].len-1<0||s[p-tr[v].len-1]!=s[p]){
            v=tr[v].fail;
        }
        return v;
    }
    void insert(char ch,int pos){
        u=get_fail(u,pos);
        if(!tr[u].to[ch-'a']){
            tr[++tot].fail=tr[get_fail(tr[u].fail,pos)].to[ch-'a'];
            tr[u].to[ch-'a']=tot;
            tr[tot].len=tr[u].len+2;
            tr[tot].cnt=tr[tr[tot].fail].cnt+1;
        }
        u=tr[u].to[ch-'a'];
    }
}PAM;

SA

int n,m,sa[N],fir[N],sec[N],t[N],rk[N];
int height[N],H[N];
char s[N];
//sa[i] 排名为 i 的后缀是以第 sa[i] 字符开始的后缀
//rk[i] 以第 sa[i] 字符开始的后缀的排名
//height[i] 后缀 i 与排名在他前面一个的后缀的 LCP(longest common prefix)
//H[i] 排名为 i 与 i − 1 的串的 LCP
void SA(){
    m=122;
    for(int i=1;i<=m;i++) t[i]=0;
    for(int i=1;i<=n;i++) t[fir[i]=s[i]]++;
    for(int i=2;i<=m;i++) t[i]+=t[i-1];
    for(int i=n;i>=1;i--) sa[t[fir[i]]--]=i;
    for(int k=1;k<=n;k<<=1){
        int cnt=0;
        for(int i=n-k+1;i<=n;i++) sec[++cnt]=i;
        for(int i=1;i<=n;i++) if(sa[i]>k) sec[++cnt]=sa[i]-k;
        for(int i=1;i<=m;i++) t[i]=0;
        for(int i=1;i<=n;i++) t[fir[i]]++;
        for(int i=2;i<=m;i++) t[i]+=t[i-1];
        for(int i=n;i>=1;i--) sa[t[fir[sec[i]]]--]=sec[i],sec[i]=0;
        for(int i=1;i<=n;i++) swap(fir[i],sec[i]);
        cnt=fir[sa[1]]=1;
        for(int i=2;i<=n;i++){
            fir[sa[i]]=(sec[sa[i]]==sec[sa[i-1]]&&sec[sa[i]+k]==sec[sa[i-1]+k])?cnt:++cnt;
        }
        m=cnt;if(cnt==n) break;
    }
}
void GetHeight(){
    for(int i=1;i<=n;i++){
        rk[sa[i]]=i;
    }
    for(int i=1,k=0;i<=n;i++){
        if(k) k--;
        if(rk[i]==1){
            height[i]=0;
            H[rk[i]]=0;//排名为 1 的 height 和 H 不重要，该部分为人为规定
            continue;
        }
        int j=sa[rk[i]-1];
        while(s[i+k]==s[j+k]) k++;
        height[i]=k;
        H[rk[i]]=k;
    }
}
//先 SA()，再 GetHeight()

SAM

string s;
struct Suffix_Automaton{
    int to[N*2][26],fa[N*2],l[N*2];//fa 和 lnk 是一个东西
    int tot,last;
    int cnt[N*2];

    Suffix_Automaton(){
        fa[0]=-1;
    }
    void add(int c){
        int p=last,np=++tot;
        // for(int i=0;i<26;i++) to[np][i]=0;
        l[np]=l[p]+1;last=np;cnt[np]=1;
        while(p!=-1&&!to[p][c]){
            to[p][c]=np;
            p=fa[p];
        }
        if(p==-1) fa[np]=0;
        else{
            int q=to[p][c];
            if(l[q]==l[p]+1) fa[np]=q;
            else{
                int nq=++tot;
                l[nq]=l[p]+1;
                for(int i=0;i<26;i++) to[nq][i]=to[q][i];
                fa[nq]=fa[q];fa[np]=fa[q]=nq;
                while(p!=-1&&to[p][c]==q){
                    to[p][c]=nq;
                    p=fa[p];
                }
            }
        }
    }
    vector<int> vec[N];
    void topu(){
        for(int i=1;i<=tot;i++) vec[l[i]].pb(i);
        for(int i=s.length();i>=1;i--){
            for(auto u:vec[i]){
                cnt[fa[u]]+=cnt[u];
            }
        }
    }
}SAM;

广义 SAM（离线 BFS 版）

#include <bits/stdc++.h>
#define pb push_back
#define ll long long
#define fi first
#define se second
#define pi pair<int,int>
using namespace std;
const int N=1e6+10;
string s;
struct Suffix_Automaton{
    int to[N*2][26],fa[N*2],l[N*2];//fa 和 lnk 是一个东西
    int tot;
    int cnt[N*2];

    Suffix_Automaton(){
        fa[0]=-1;
    }
    int add(int c,int last){
        int p=last,np=++tot;
        // for(int i=0;i<26;i++) to[np][i]=0;
        l[np]=l[p]+1;last=np;cnt[np]=1;
        while(p!=-1&&!to[p][c]){
            to[p][c]=np;
            p=fa[p];
        }
        if(p==-1){
            fa[np]=0;
            return np;
        }
        else{
            int q=to[p][c];
            if(l[q]==l[p]+1){
                fa[np]=q;
                return np;
            }
            else{
                int nq=++tot;
                l[nq]=l[p]+1;
                for(int i=0;i<26;i++) to[nq][i]=to[q][i];
                fa[nq]=fa[q];fa[np]=fa[q]=nq;
                while(p!=-1&&to[p][c]==q){
                    to[p][c]=nq;
                    p=fa[p];
                }
            }
        }
        return np;
    }

    vector<int> vec[N];
    void topu(){
        for(int i=1;i<=tot;i++) vec[l[i]].pb(i);
        for(int i=s.length();i>=1;i--){
            for(auto u:vec[i]){
                cnt[fa[u]]+=cnt[u];
            }
        }
    }
}SAM;
struct Trie{
    struct Trie_Tree{
        int fail,to[26],ans;
        int c,fa;
    }tr[N];
    int match[N],tot,in[N];
    void insert(string s,int k){
        int l=s.length();
        int u=0;
        for(int i=0;i<l;i++){
            if(!tr[u].to[s[i]-'a']){
                tr[u].to[s[i]-'a']=++tot;
                tr[tot].c=s[i]-'a';
                tr[tot].fa=u;
            }
            u=tr[u].to[s[i]-'a'];
        }
        match[k]=u;
    }
    int pos[N];
    void construct(){
        queue<int> q;
        for(int i=0;i<26;i++){
            if(tr[0].to[i]){
                tr[tr[0].to[i]].fail=0;
                q.push(tr[0].to[i]);
            }
        }
        pos[0]=0;
        while(!q.empty()){
            int u=q.front();q.pop();
            pos[u]=SAM.add(tr[u].c,pos[tr[u].fa]);
            for(int i=0;i<26;i++){
                if(tr[u].to[i]){
                    q.push(tr[u].to[i]);
                }
            }
        }
    }
}Trie;
int n;
int main() {
    scanf("%d",&n);
    for(int i=1;i<=n;i++){
        cin>>s;
        Trie.insert(s,i);
    }
    Trie.construct();
    ll ans=0;
    for(int i=1;i<=SAM.tot;i++){
        ans+=SAM.l[i]-SAM.l[SAM.fa[i]];
    }
    printf("%lld\n%lld\n",ans,SAM.tot+1);
    return 0;
}

广义 SAM（在线版）

#include <bits/stdc++.h>
#define pb push_back
#define ll long long
#define fi first
#define se second
#define pi pair<int,int>
using namespace std;
const int N=1e6+10,inf=2*N-1;
string s;
struct Suffix_Automaton{
    int to[N*2][26],fa[N*2],l[N*2];//fa 和 lnk 是一个东西
    int tot;
    int cnt[N*2];

    Suffix_Automaton(){
        fa[0]=-1;
    }
    int add(int c,int last){
        if(to[last][c] && l[to[last][c]]==l[last]+1){
            return to[last][c];
        }
        int p=last,np=++tot,nq;
        bool flag=0;
        l[np]=l[p]+1;cnt[np]=1;
        while(p!=-1&&!to[p][c]){
            to[p][c]=np;
            p=fa[p];
        }
        if(p==-1){
            fa[np]=0;
            return np;
        }
        else{
            int q=to[p][c];
            if(l[q]==l[p]+1){
                fa[np]=q;
                return np;
            }
            else{
                if(p==last){
                    flag=1,np=inf,tot--;
                }
                nq=++tot;
                l[nq]=l[p]+1;
                for(int i=0;i<26;i++) to[nq][i]=to[q][i];
                fa[nq]=fa[q];fa[np]=fa[q]=nq;
                while(p!=-1&&to[p][c]==q){
                    to[p][c]=nq;
                    p=fa[p];
                }
            }
        }
        return flag?nq:np;
    }

    vector<int> vec[N];
    void topu(){
        for(int i=1;i<=tot;i++) vec[l[i]].pb(i);
        for(int i=s.length();i>=1;i--){
            for(auto u:vec[i]){
                cnt[fa[u]]+=cnt[u];
            }
        }
    }
}SAM;
int n;
int pos[N];
int main() {
    scanf("%d",&n);
    for(int i=1;i<=n;i++){
        cin>>s;
        for(int j=0;j<s.length();j++){
            if(j==0) pos[j]=SAM.add(s[j]-'a',0);
            else pos[j]=SAM.add(s[j]-'a',pos[j-1]);
        }
    }
    ll ans=0;
    for(int i=1;i<=SAM.tot;i++){
        ans+=SAM.l[i]-SAM.l[SAM.fa[i]];
    }
    printf("%lld\n%lld\n",ans,SAM.tot+1);
    return 0;
}
本文作者：water_tomato
AC 自动机ACMBorder 树ICPCkmpLCPManacherPAMTrie 树后缀数组后缀自动机字符串字符串匹配字符串哈希模板算法

评论

  1. 514imb
    3 月前
    2024-9-05 17:34:55

    orz

    • water_tomato
      博主
      514imb
      3 月前
      2024-9-05 17:36:16

      洛谷小学生标准语句(bushi

发送评论 编辑评论

 
 
 
 
 
 
 
  
  
   
|´・ω・)ノ
ヾ(≧∇≦*)ゝ
(☆ω☆)
（╯‵□′）╯︵┴─┴
￣﹃￣
(/ω＼)
∠( ᐛ 」∠)＿
(๑•̀ㅁ•́ฅ)
→_→
୧(๑•̀⌄•́๑)૭
٩(ˊᗜˋ*)و
(ノ°ο°)ノ
(´இ皿இ｀)
⌇●﹏●⌇
(ฅ´ω`ฅ)
(╯°A°)╯︵○○○
φ(￣∇￣o)
ヾ(´･ ･｀｡)ノ"
( ง ᵒ̌皿ᵒ̌)ง⁼³₌₃
(ó﹏ò｡)
Σ(っ °Д °;)っ
( ,,´･ω･)ﾉ"(´っω･｀｡)
╮(╯▽╰)╭
o(*////▽////*)q
＞﹏＜
( ๑´•ω•) "(ㆆᴗㆆ)
😂
😀
😅
😊
🙂
🙃
😌
😍
😘
😜
😝
😏
😒
🙄
😳
😡
😔
😫
😱
😭
💩
👻
🙌
🖕
👍
👫
👬
👭
🌚
🌝
🙈
💊
😶
🙏
🍦
🍉
😣
Source: github.com/k4yt3x/flowerhd
颜文字
Emoji
小恐龙
花!
  
上一篇
下一篇