也只有我这种蒟蒻会现在才学平衡树吧……
本博客参考:PoPoQQQ 和 nzhtl1477 的课件;do_while_true, hzwer, 皎月半洒花 和 yybyyb 的代码启发
其实“参考”也就是我本人在学习时使用的资料。
前置 – 二叉搜索树(BST)
模板题:Luogu5076
关键性质:一个节点 $x$ 左子树所有点的关键字都比 $x$ 的关键字小,右子树所有点的关键字都比 $x$ 的关键字大。
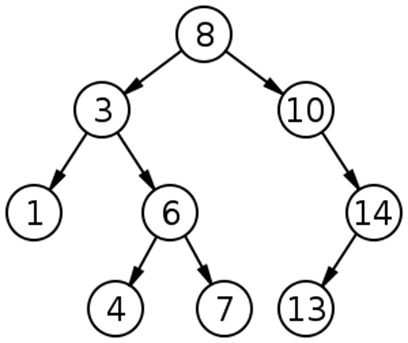
支持:查询 $x$ 数的排名,查询排名为 $x$ 的数($k$ 大值),求 $x$ 的前驱/后继,插入 $x$。
缺陷:按从小到大顺序插入值,复杂度会退化;不容易实现删除操作。
二叉搜索树(Binary Search Tree,以下简称 BST)的缺陷决定了这个算法必须被优化或取代,但是,由于平衡树的许多操作是与二叉平衡树相通(甚至相同)的,所以学习二叉平衡树非常有必要。
下面给出 BST 的的基本构造:
struct node{
int val,w,ls,rs,siz;//分别代表:关键字,关键字出现次数,左/右儿子,以该点为根的子树的大小(简称节点大小/子树大小)
}tree[N];
由于一个值可能会出现多次,如果分成多个点会造成不必要的麻烦,因为我们用 $w$ 记录同一个值的出现次数,用一个点记录下来。
由于 BST 比较容易理解,这里不再过度阐述,结合代码来简单阐述每一种操作。
插入
inline void insert(int v,int x){
tree[x].siz++;//大小加 1
if(tree[x].val==v){//要插入的这个值已存在并且找到,直接 w++
tree[x].w++;
return;
}
if(tree[x].val>v){//要插入的值较小,往左儿子走
if(tree[x].ls!=0) insert(v,tree[x].ls);
else{//没有左儿子,创建一个新点
tree[++cnt].val=v;
tree[cnt].siz=tree[cnt].w=1;
tree[x].ls=cnt;
}
}
else{//往右儿子走
if(tree[x].rs!=0) insert(v,tree[x].rs);
else{//同上
tree[++cnt].val=v;
tree[cnt].siz=tree[cnt].w=1;
tree[x].rs=cnt;
}
}
}
特别的,如果插入数时 BST 尚是空的,需要特判一下,然后执行以下代码即可:
tree[++cnt].val=x;
tree[cnt].siz=tree[cnt].w=1;
查询数 $x$ 的排名
inline int queryrk(int v,int x){
if(x==0) return 0;//找到尽头,返回 0,不可省略
if(tree[x].val==v) return tree[tree[x].ls].siz;//找到这个数,返回左儿子的大小
if(v<tree[x].val) return queryrk(v,tree[x].ls);//小于当前位置,向左儿子走
return tree[tree[x].ls].siz+tree[x].w+queryrk(v,tree[x].rs);//向右儿子走的同时,左儿子以及当前位置均比查询的数小,因此全部需要纳入答案中
}
注意,这里找到的排名实际为排名 $-1$ 的值(结合代码自行理解),所以如果要输出排名,代码应该为 printf("%d\n",queryrk(x,1)+1);
查询排名为 $x$ 的数(求 $k$ 大值)
inline int querynum(int rk,int x){
if(x==0) return 0;//找到尽头,返回 0,若必然找得到,可省略
if(tree[tree[x].ls].siz>=rk) return querynum(rk,tree[x].ls);
if(tree[tree[x].ls].siz+tree[x].w>=rk) return tree[x].val;
return querynum(rk-tree[tree[x].ls].siz-tree[x].w ,tree[x].rs);//上边两行都不满足,则相当于查询右儿子中排名为 rk-tree[tree[x].ls].siz-tree[x].w 的数
}
求 $x$ 的前驱/后继
前驱定义为小于 $x$,且最大的数;后继定义为大于 $x$,且最小的数。
inline int queryfr(int v,int ans,int x){//查询前驱
if(tree[x].val>=v){//当前位置不小于 x,去左子树找找有没有小于的
if(!tree[x].ls) return ans;//没有左子树,返回当前找到的合法的最大值
return queryfr(v,ans,tree[x].ls);
}
else{//当前位置小于 x,是合法的
if(!tree[x].rs) return tree[x].val;//没有右儿子,由于当前位置的左儿子一定小于当前位置,所以既然当前位置合法,就一定是当前位置的值
return queryfr(v,tree[x].val,tree[x].rs);//有右儿子,找找右儿子里有没有更大的合法的数
}
}
inline int queryne(int v,int ans,int x){//查询后继
if(tree[x].val<=v){//前驱的逆运算,原理类似,不再重复阐述
if(!tree[x].rs) return ans;
return queryne(v,ans,tree[x].rs);
}
else{
if(!tree[x].ls) return tree[x].val;
return queryne(v,tree[x].val,tree[x].ls);
}
}
至此,二叉搜索树的基本内容就结束了,在此基础上进行优化,也就来到了平衡树的内容。
平衡树的基本定义:利用旋转操作通过一些手段保证 BST 的复杂度不会退化的 BST 结构。
同时,平衡树也相对更能够支持删除操作。定义还告诉我们,平衡树的本质仍然是 BST,而旋转操作,也是平衡树学习的重点。
在 OI 中最常用的平衡树是 Treap 和 Splay,本文也仅仅对这两种平衡树进行说明(实际上我也就学了这两种平衡树ovo)。
Treap
tree(树)+heap(堆)=treap
顾名思义,treap 就是利用堆的性质来维护平衡的一种平衡树。核心思想就是:给每个点随机分配一个权值,使 treap 同时满足堆性质和二叉搜索树性质,这样可以使得树高期望保证在 $O(\log n)$,容易知道,treap 除了 BST 需要维护的信息以外,还需要额外维护一个堆随机值。
具体地说:
设每个节点的关键字是 $key$,随机权值是 $rnd$。
- 如果 $v$ 是 $u$ 的左儿子,则 $key_v < key_u$;
- 如果 $v$ 是 $u$ 的右儿子,则 $key_v > key_u$;
- 如果 $v$ 是 $u$ 的子节点,则 $rnd_u > rnd_v$。
要维护的信息具体如下:
struct node{
int ls,rs,w,siz,val,rnd;//rnd 为随机权值
}tr[N];
问题是如何使其同时满足堆性质和二叉搜索树性质呢?接着就是平衡树的核心——旋转操作。
旋转
旋转分为单旋和双旋,在 treap 中,只需要用到单旋(双旋会在 Splay 中阐述)。
单旋中又包含左旋和右旋,两者是互逆的。
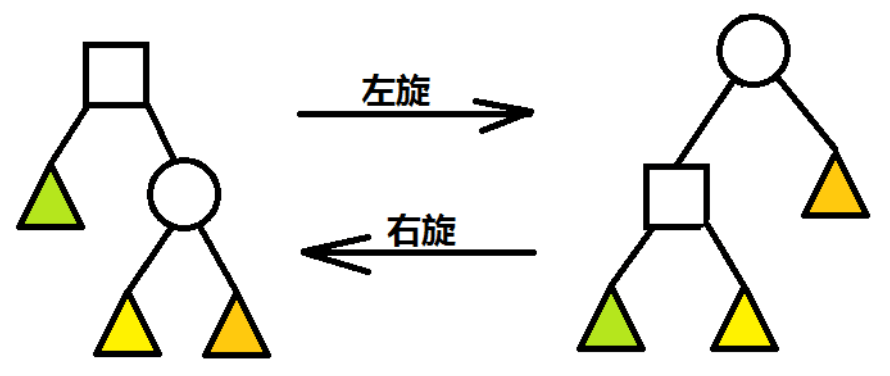
用文字阐述就是:
左旋:将右儿子提到当前节点,自己作为右儿子的左儿子,右儿子原来的左儿子变成自己新的右儿子
右旋:将左儿子提到当前节点,自己作为左儿子的右儿子,左儿子原来的右儿子变成自己新的左儿子
为什么旋转操作非常重要?因为旋转有一个绝妙的性质——旋转后的二叉树仍满足二叉搜索树的条件。因此我们可以利用旋转操作来使 treap 满足堆性质,同时不破坏 BST 的性质。
旋转操作的代码如下:
inline void update(int x){//更新子树大小
tr[x].siz=tr[tr[x].ls].siz+tr[tr[x].rs].siz+tr[x].w;
}
inline void rturn(int &x){//右旋
int t=tr[x].ls;tr[x].ls=tr[t].rs;tr[t].rs=x;
tr[t].siz=tr[x].siz;update(x);x=t;
}
inline void lturn(int &x){//左旋
int t=tr[x].rs;tr[x].rs=tr[t].ls;tr[t].ls=x;
tr[t].siz=tr[x].siz;update(x);x=t;
}//x 一定要加 &,这样可以在更改 x 的值时同时修改之前的 ls/rs,结合插入/删除操作理解
treap 查询排名/$k$ 大值/前驱/后继的方法与 BST 完全相同,不再阐述,将会在文末贴出完整代码。
插入
treap 的插入操作与 BST 的差异保证了其复杂度不会退化,即:像 BST 那样插入,回溯时通过旋转来调整,使其满足堆性质。
inline void insert(int &x,int v){//&x 理由同上
if(x==0){//找到了一个尚无的节点,插入
cnt++;x=cnt;
tr[x].siz=tr[x].w=1;
tr[x].val=v;tr[x].rnd=rand();
return;
}
tr[x].siz++;
if(tr[x].val==v){
tr[x].w++;
return;
}
if(v>tr[x].val){
insert(tr[x].rs,v);
if(tr[tr[x].rs].rnd<tr[x].rnd) lturn(x);//插入完回溯的时候,需要看看需不需要旋转以满足堆性质,这里是以小根堆为例的,大根堆也可以
}
else{
insert(tr[x].ls,v);
if(tr[tr[x].ls].rnd<tr[x].rnd) rturn(x);//同上
}
}
删除
删除操作在平衡树中尤为重要。首先先用 BST 的方式找到要删除的数所在的节点(以下称为“当前节点”),然后:
- 若当前节点数值的出现次数大于 $1$ ,则将数值出现次数减 $1$ 即可。
- 若当前节点数值的出现次数等于 $1$ :
- 若当前节点没有左儿子与右儿子,则直接删除该节点;
- 若当前节点只有左儿子/右儿子,则用左儿子/右儿子替代该节点;
- 若当前节点有左儿子与右儿子,则不断旋转当前节点,并走到当前节点新的对应位置,直到当前节点只有左儿子/右儿子为止。
inline void del(int &x,int v){//同上
if(x==0) return;
if(tr[x].val==v){//找到了要删除的数
if(tr[x].w>1){//出现次数大于 1 ,直接 -1
tr[x].w--;tr[x].siz--;return;
}
if(tr[x].ls==0||tr[x].rs==0) x=tr[x].ls+tr[x].rs;//只有左儿子/右儿子,取而代之即可
else if(tr[tr[x].ls].rnd<tr[tr[x].rs].rnd){//左右儿子都有,开始不断旋转
rturn(x);//旋转时不仅需要满足 BST 性质,
del(x,v);//还需要满足堆性质(即判断 rnd 的大小再决定怎么旋转,
}//显然小堆顶情况下,需要让 rnd 小的旋转上来)
else{
lturn(x);
del(x,v);
}
}
else if(v>tr[x].val){//找要删除的数
tr[x].siz--;del(tr[x].rs,v);
}
else{
tr[x].siz--;del(tr[x].ls,v);
}
}
至此,我们实现了最基本的 treap ,完整代码会在文末代码部分贴出。
Splay
模板题:Luogu3391
Splay,又称文艺平衡树。Splay 对一个节点进行操作的时候通过一种方法把这个点旋转至根(即 splay 操作),从而保证了平衡。Splay 的复杂度证明非常复杂(显然我也不会),故不作阐述。
为了简单说明在学会了 treap 情况下 Splay 的用途和不足,下面引用一段 nzhtl1477 的话:
Advantage:
Splay具有“自适应性”
大概就是说splay会根据操作的特点调整树结构,使得操作尽可能高效
可以去了解了解splay的动态最优性猜想,是个著名的open problem由于自适应性,splay不需要特殊的技巧就可以高效启发式合并,还可以高效实现LCT(STT)等动态树
Disadvantage:
可以通过势能分析证明splay的复杂度是均摊O( logn )的,也就是说splay在很多次操作中可能会有一次 $O( n )$ 复杂度的操作,而且这样的操作也很好构造,所以splay不适合做一些需要撤销操作/可持久化的题目(虽然可以通过随机旋转什么的方法来规避,但还是感觉很吃力)
自身常数比较大
单旋操作的 Splay 复杂度无法保证,因此我们需要通过双旋操作来保证其复杂度(同样不会证明)。
如果对证明非常感兴趣,可以看 delayyy 的课件:http://delayyy.blog.uoj.ac/blog/90
由于双旋(下文会阐述)中需要父亲/祖父的参与,因此我们除了 BST 中需要维护的以外,我们还需要维护每一个节点的父亲节点。
struct Splay_Tree{
int son[2],fa,cnt,val,siz;//son0=ls son1=rs
}tree[N];
Splay 的代码和 treap 不是同一天打的,打 Splay 的时候发现原先 ls,rs 的标法对打代码造成了非常大的麻烦(看下去就知道了),所以改用了主流的 son[2]
双旋
先上文字阐述:
讨论 $x$ 和父亲的关系与 $x$ 父亲和祖父的关系是否相同(换句话说 $x$-父亲-祖父是不是直的)
- $x$ 的父亲是根:旋转一次到根;
- $x$ 是父亲的左/右儿子且 $x$ 父亲是 $x$ 祖父的左/右儿子:先右/左旋祖父,再右/左旋父亲(下方第一张图);
- $x$ 是父亲的左/右儿子但 $x$ 父亲是 $x$ 祖父的右/左儿子:先右/左旋父亲,再左/右旋祖父(下方第二张图)。
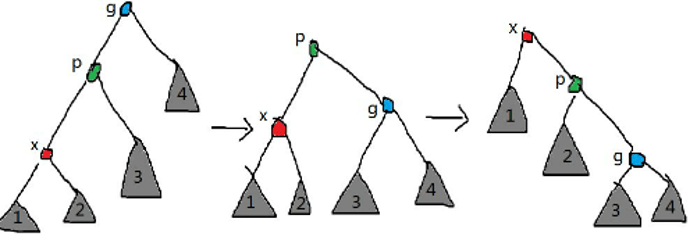
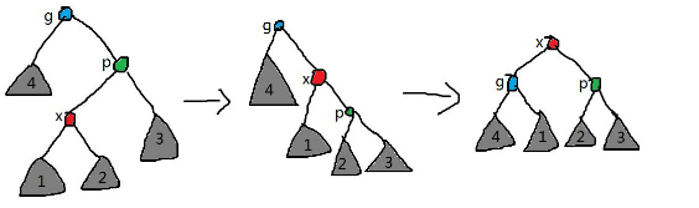
代码和 splay 操作一起讲。
splay 操作
为了阐述清晰,我胡乱规定该数据结构用 Splay 表示,该操作用 splay 操作表示(没有任何道理,纯粹是为了防止混淆)。
定义:将节点 $x$ 通过旋转操作旋转到根的位置。
接着直接结合代码来看。
inline void update(int u){//更新节点大小
tree[u].siz=tree[tree[u].son[0]].siz+tree[tree[u].son[1]].siz+tree[u].cnt;
}
inline bool check(int u){//判断左/右儿子,左儿子返回 0,右儿子返回 1
return tree[tree[u].fa].son[1]==u;
}
inline void rotate(int u){//将 u 旋转上去,这个定义和我写的 treap 略有不同
int fa=tree[u].fa;
int ffa=tree[fa].fa;
int k=check(u);
tree[ffa].son[check(fa)]=u;tree[u].fa=ffa;//各种更新父亲不要漏了
tree[fa].son[k]=tree[u].son[k^1];tree[tree[u].son[k^1]].fa=fa;
tree[u].son[k^1]=fa;tree[fa].fa=u;
update(fa);update(u);//先更新 fa ,理由显然
}
inline void splay(int u,int goal){//将节点 u 旋转到父亲为 goal 为止
while(tree[u].fa!=goal){//没到
int fa=tree[u].fa;
int ffa=tree[fa].fa;
if(ffa!=goal){//祖父不是目标,它就要被转
if(check(u)==check(fa)) rotate(fa);//判断先转父亲还是先转 u
else rotate(u);
}
rotate(u);//第二步肯定是转 u
}
if(!goal) root=u;
}
而这个操作也是我们保证 Splay 复杂度的关键,每对一个节点进行操作的时候我们都 splay 一下把该节点变成根,复杂度就得到了保证,代码与 BST 较为类似,就是多了一行 splay 操作,这里不再阐述插入/删除/查询等操作。
建树
阐述 treap 的时候,我们是对一个个值进行维护,而在 Splay 模板题中,我们需要对于一个区间进行维护,因此首先就需要对这一个区间建树(关键字就是在区间中的位置)。这部分比较简单,不多做阐述,略做修改也可以成为 treap 的建树方法。
inline int build(int l,int r,int fa){//简单递归建树
if(l>r) return 0;
int v=++cnt;
tree[v].fa=fa;
tree[v].cnt=1;
int mid=(l+r)>>1;
tree[v].val=a[mid];//权值就是 mid 的原始值
tree[v].son[0]=build(l,mid-1,v);
tree[v].son[1]=build(mid+1,r,v);
update(v);
return v;
}
容易知道,所得到的二叉树的中序遍历就是原序列(最终的中序遍历就是最终序列)。
原因:本模板题中,关键字实际上就是在当前序列中的序号,由于在 BST 中中序遍历会以关键字从小到大遍历,因而中序遍历得到的结果就是真实序列。
区间翻转
区间翻转就是模板题给我们要求,也是 treap 难以实现而 Splay 较容易实现的一项操作,是 Splay 的优势之一。
对于每次翻转区间 $[l,r]$,我们利用 Splay 的特性,运用 splay 操作,将 $l-1$ 旋转到根节点,再将 $r+1$ 旋转到根节点的右儿子,这样,$r+1$ 的左儿子代表的子树显然就是 $[l,r]$。
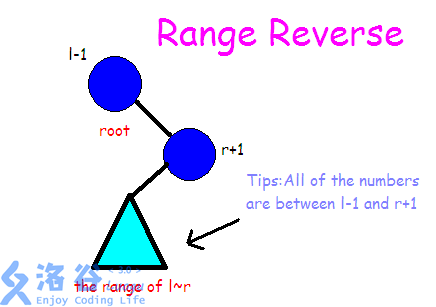
之后我们只需要给 $r+1$ 的左儿子打上一个翻转的 tag (即,交换左右儿子)并依次传递下去即可。容易发现,一层一层交换之后,二叉树的中序遍历就成功反过来了,也就是说成功完成了序列翻转。
inline void pushdown(int x){
if(tree[x].tag){
tree[tree[x].son[0]].tag^=1;
tree[tree[x].son[1]].tag^=1;
swap(tree[x].son[0],tree[x].son[1]);//交换左右儿子
tree[x].tag=0;
}
}
inline int query(int rk){//查询第 k 大的数的位置,由于权值为在序列中的序号,所以后第 k 大也就是在序列中的第 k 个数
int u=root;
pushdown(u);//一边找一边要 pushdown
while(1){
if(tree[tree[u].son[0]].siz>=rk){
u=tree[u].son[0];
}
else if(tree[tree[u].son[0]].siz+tree[u].cnt>=rk) return u;
else{
rk-=tree[tree[u].son[0]].siz+tree[u].cnt;
u=tree[u].son[1];
}
pushdown(u);
}
}
inline void reverse(int l,int r){
l=query(l-1);r=query(r+1);//找到序列中第 l-1 个数和第 r+1 个数的位置
splay(l,0);splay(r,l);//如上图
int tmp=tree[r].son[0];//找到上图中三角形那个子树,打上翻转 tag
tree[tmp].tag^=1;
}
对于这道模板题,再进行了全部翻转之后,最后中序遍历一次输出结果即可,这里不再做细节的阐述。
至此,Luogu3391 就被解决了,我们接着给出 Splay 中其他操作的代码。
与 treap 的递归写法不同,Splay 我采用了循环写法,思想类似,但个人写 Splay 的时候发觉循环写着比较容易,就写了循环(treap 在 insert 中需要递归回来进行旋转,故递归写法更合适些,而查询等与 BST 类似的操作同样可以用循环写法)。
查询排名为 $x$ 的数就是上边代码中的 query,不再重复。
插入
inline void insert(int x){
int u=root,fa=0;
while(tree[u].val!=x&&u){
fa=u;
u=tree[u].son[x>tree[u].val];//判断往左儿子走还是往右儿子走
}
if(u) tree[u].cnt++;
else{
u=++cnt;
if(fa) tree[fa].son[x>tree[fa].val]=u;
tree[u].fa=fa;tree[u].val=x;
tree[u].cnt=tree[u].siz=1;
}
splay(u,0);//插入完了 splay 一下
}
查询 $x$ 数的排名
这个操作比较有意思,实现方法就是把 $x$ 数旋转到根上来,然后直接回答左儿子的大小(当然还要判断一下根节点,因为询问的数不一定存在)。
实际上,find 函数在查找前驱/后继时也有用,看下去即可明白。
inline void find(int x){
int u=root;
while(x!=tree[u].val&&tree[u].son[x>tree[u].val]){
u=tree[u].son[x>tree[u].val];
}
splay(u,0);
}
………………
find(x);
int tmp=tree[tree[root].son[0]].siz;//见下面小 tip
if(tree[root].val<x) tmp+=tree[root].cnt;
printf("%d\n",tmp);
小 Tip
Splay 还有一个小 tip,因为它天旋地转的,所以建议在操作之前先 insert(-inf);insert(inf); 防止旋转时跑丢(比如翻转区间时,如果翻转的是整个区间,没有这俩就会出问题)。同时,由于这两个数,代码细节上会有些许改变,比如查询排名时不需要再 $+1$,原因显然。
求 $x$ 的前驱/后继
对于这个操作,我们先把 $x$ 找到并旋转到根节点,那么前驱显然就是左子树中最右的,后继反之。
inline int frne(int x,int opt){//opt=0 前驱,opt=1 后继
find(x);//看前面
int u=root;
if((!opt&&tree[u].val<x)||(opt&&tree[u].val>x)) return u;
u=tree[u].son[opt];//向左子树走
while(tree[u].son[opt^1]) u=tree[u].son[opt^1];//然后一直往右
return u;
}
删除
学习了前边两个,才可以学习删除操作。Splay 中的删除操作比较特殊,先找到 $x$ 的前驱和后继(显然 $x$ 就是被夹在中间的糕点),然后像区间翻转时的操作那样,把前驱翻转到根,后继反转到根的右儿子,然后后继的左儿子自然就是要删除的那个数了。
inline void del(int x){
int l=frne(x,0);//看前面
int r=frne(x,1);
splay(l,0);splay(r,l);
int tmp=tree[r].son[0];
if(tree[tmp].cnt>1){//同样要分类
tree[tmp].cnt--;
splay(tmp,0);
}
else tree[r].son[0]=0;
}
这样 Splay 就学完啦!与 treap 不同,Splay 通过 splay 操作可以玩出很多花样(看独特的删除和找前驱/后继就知道啦),虽然似乎跑的比 treap 慢一点,但是却是一个延展性很大的算法。
一道练手题
Luogu2042 [NOI2005] 维护数列 平衡树维护数列,考察 Splay,思维难度不大但代码挺长的,适合练手以加深理解。
最后在文末给出本文中 Luogu3369 和 Luogu3391 两道模板题的 AC 代码。
完整代码(无注释)
Luogu3369 【模板】普通平衡树 – 使用 Treap 实现
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
const int inf=2147483647;
struct node{
int ls,rs,w,siz,val,rnd;
}tr[N];
int n,cnt,root,tot;
inline void update(int x){
tr[x].siz=tr[tr[x].ls].siz+tr[tr[x].rs].siz+tr[x].w;
}
inline void rturn(int &x){
int t=tr[x].ls;tr[x].ls=tr[t].rs;tr[t].rs=x;
tr[t].siz=tr[x].siz;update(x);x=t;
}
inline void lturn(int &x){
int t=tr[x].rs;tr[x].rs=tr[t].ls;tr[t].ls=x;
tr[t].siz=tr[x].siz;update(x);x=t;
}
inline void insert(int &x,int v){
if(x==0){
cnt++;x=cnt;
tr[x].siz=tr[x].w=1;
tr[x].val=v;tr[x].rnd=rand();
return;
}
tr[x].siz++;
if(tr[x].val==v){
tr[x].w++;
return;
}
if(v>tr[x].val){
insert(tr[x].rs,v);
if(tr[tr[x].rs].rnd<tr[x].rnd) lturn(x);
}
else{
insert(tr[x].ls,v);
if(tr[tr[x].ls].rnd<tr[x].rnd) rturn(x);
}
}
inline void del(int &x,int v){
if(x==0) return;
if(tr[x].val==v){
if(tr[x].w>1){
tr[x].w--;tr[x].siz--;return;
}
if(tr[x].ls==0||tr[x].rs==0) x=tr[x].ls+tr[x].rs;
else if(tr[tr[x].ls].rnd<tr[tr[x].rs].rnd){
rturn(x);
del(x,v);
}
else{
lturn(x);
del(x,v);
}
}
else if(v>tr[x].val){
tr[x].siz--;del(tr[x].rs,v);
}
else{
tr[x].siz--;del(tr[x].ls,v);
}
}
inline int queryrk(int x,int v){
if(x==0) return 0;
if(tr[x].val==v) return tr[tr[x].ls].siz;
if(v>tr[x].val) return tr[tr[x].ls].siz+tr[x].w+queryrk(tr[x].rs,v);
return queryrk(tr[x].ls,v);
}
inline int querynum(int x,int rk){
if(x==0) return 0;
if(rk<=tr[tr[x].ls].siz) return querynum(tr[x].ls,rk);
if(rk<=tr[tr[x].ls].siz+tr[x].w) return tr[x].val;
return querynum(tr[x].rs,rk-tr[tr[x].ls].siz-tr[x].w);
}
inline int queryfr(int x,int v,int ans){
if(tr[x].val>=v){
if(!tr[x].ls) return ans;
return queryfr(tr[x].ls,v,ans);
}
else{
if(!tr[x].rs) return tr[x].val;
return queryfr(tr[x].rs,v,tr[x].val);
}
}
inline int queryne(int x,int v,int ans){
if(tr[x].val<=v){
if(!tr[x].rs) return ans;
return queryne(tr[x].rs,v,ans);
}
else{
if(!tr[x].ls) return tr[x].val;
return queryne(tr[x].ls,v,tr[x].val);
}
}
int main(){
scanf("%d",&n);
for(int i=1,opt,x;i<=n;i++){
scanf("%d%d",&opt,&x);
if(opt==1){
if(tot==0){
cnt++;
root=cnt;
tr[cnt].siz=tr[cnt].w=1;
tr[cnt].val=x;tr[cnt].rnd=rand();
}
else insert(root,x);
tot++;
}
else if(opt==2){
del(root,x);
tot--;
}
else if(opt==3) printf("%d\n",queryrk(root,x)+1);
else if(opt==4) printf("%d\n",querynum(root,x));
else if(opt==5) printf("%d\n",queryfr(root,x,-inf));
else printf("%d\n",queryne(root,x,inf));
}
return 0;
}
Luogu3369 【模板】普通平衡树 – 使用 Splay 实现
#include<bits/stdc++.h>
using namespace std;
const int N=5e5+5;
struct Splay_Tree{
int son[2],fa,cnt,val,siz;
}tree[N];
int n,root,cnt;
const int inf=2147483647;
inline void update(int u){
tree[u].siz=tree[tree[u].son[0]].siz+tree[tree[u].son[1]].siz+tree[u].cnt;
}
inline bool check(int u){
return tree[tree[u].fa].son[1]==u;
}
inline void rotate(int u){
int fa=tree[u].fa;
int ffa=tree[fa].fa;
int k=check(u);
tree[ffa].son[check(fa)]=u;tree[u].fa=ffa;
tree[fa].son[k]=tree[u].son[k^1];tree[tree[u].son[k^1]].fa=fa;
tree[u].son[k^1]=fa;tree[fa].fa=u;
update(fa);update(u);
}
inline void splay(int u,int goal){
while(tree[u].fa!=goal){
int fa=tree[u].fa;
int ffa=tree[fa].fa;
if(ffa!=goal){
if(check(u)==check(fa)) rotate(fa);
else rotate(u);
}
rotate(u);
}
if(!goal) root=u;
}
inline void insert(int x){
int u=root,fa=0;
while(tree[u].val!=x&&u){
fa=u;
u=tree[u].son[x>tree[u].val];
}
if(u) tree[u].cnt++;
else{
u=++cnt;
if(fa) tree[fa].son[x>tree[fa].val]=u;
tree[u].fa=fa;tree[u].val=x;
tree[u].cnt=tree[u].siz=1;
}
splay(u,0);
}
inline void find(int x){
int u=root;
while(x!=tree[u].val&&tree[u].son[x>tree[u].val]){
u=tree[u].son[x>tree[u].val];
}
splay(u,0);
}
inline int frne(int x,int opt){
find(x);
int u=root;
if((!opt&&tree[u].val<x)||(opt&&tree[u].val>x)) return u;
u=tree[u].son[opt];
while(tree[u].son[opt^1]) u=tree[u].son[opt^1];
return u;
}
inline void del(int x){
int l=frne(x,0);
int r=frne(x,1);
splay(l,0);splay(r,l);
int tmp=tree[r].son[0];
if(tree[tmp].cnt>1){
tree[tmp].cnt--;
splay(tmp,0);
}
else tree[r].son[0]=0;
}
inline int query(int rk){
int u=root;
while(1){
if(tree[tree[u].son[0]].siz>=rk){
u=tree[u].son[0];
}
else if(tree[tree[u].son[0]].siz+tree[u].cnt>=rk) return u;
else{
rk-=tree[tree[u].son[0]].siz+tree[u].cnt;
u=tree[u].son[1];
}
}
}
int main(){
insert(-inf);insert(inf);
scanf("%d",&n);
for(int i=1,opt,x;i<=n;i++){
scanf("%d%d",&opt,&x);
if(opt==1) insert(x);
else if(opt==2) del(x);
else if(opt==3){
find(x);
int tmp=tree[tree[root].son[0]].siz;
if(tree[root].val<x) tmp+=tree[root].cnt;
printf("%d\n",tmp);
}
else if(opt==4) printf("%d\n",tree[query(x+1)].val);
else if(opt==5) printf("%d\n",tree[frne(x,0)].val);
else printf("%d\n",tree[frne(x,1)].val);
}
return 0;
}
Luogu3391 【模板】文艺平衡树 – 使用 Splay 实现
#include<bits/stdc++.h>
using namespace std;
const int N=5e5+5;
struct Splay_Tree{
int son[2],fa,cnt,val,siz,tag;
}tree[N];
int n,root,cnt,m,a[N];
const int inf=2147483647;
inline void update(int u){
tree[u].siz=tree[tree[u].son[0]].siz+tree[tree[u].son[1]].siz+tree[u].cnt;
}
inline void pushdown(int x){
if(tree[x].tag){
tree[tree[x].son[0]].tag^=1;
tree[tree[x].son[1]].tag^=1;
swap(tree[x].son[0],tree[x].son[1]);
tree[x].tag=0;
}
}
inline int build(int l,int r,int fa){
if(l>r) return 0;
int v=++cnt;
tree[v].fa=fa;
tree[v].cnt=1;
int mid=(l+r)>>1;
tree[v].val=a[mid];
tree[v].son[0]=build(l,mid-1,v);
tree[v].son[1]=build(mid+1,r,v);
update(v);
return v;
}
inline bool check(int u){
return tree[tree[u].fa].son[1]==u;
}
inline void rotate(int u){
int fa=tree[u].fa;
int ffa=tree[fa].fa;
pushdown(u);pushdown(fa);
int k=check(u);
tree[ffa].son[check(fa)]=u;tree[u].fa=ffa;
tree[fa].son[k]=tree[u].son[k^1];tree[tree[u].son[k^1]].fa=fa;
tree[u].son[k^1]=fa;tree[fa].fa=u;
update(fa);update(u);
}
inline void splay(int u,int goal){
while(tree[u].fa!=goal){
int fa=tree[u].fa;
int ffa=tree[fa].fa;
pushdown(u);pushdown(fa);
if(ffa!=goal){
if(check(u)==check(fa)) rotate(fa);
else rotate(u);
}
rotate(u);
}
if(!goal) root=u;
}
inline int query(int rk){
int u=root;
pushdown(u);
while(1){
if(tree[tree[u].son[0]].siz>=rk){
u=tree[u].son[0];
}
else if(tree[tree[u].son[0]].siz+tree[u].cnt>=rk) return u;
else{
rk-=tree[tree[u].son[0]].siz+tree[u].cnt;
u=tree[u].son[1];
}
pushdown(u);
}
}
inline void getans(int x){
pushdown(x);
if(tree[x].son[0]) getans(tree[x].son[0]);
if(tree[x].val!=inf&&tree[x].val!=-inf) printf("%d ",tree[x].val);
if(tree[x].son[1]) getans(tree[x].son[1]);
}
inline void reverse(int l,int r){
l=query(l-1);r=query(r+1);
splay(l,0);splay(r,l);
int tmp=tree[r].son[0];
tree[tmp].tag^=1;
}
int main(){
scanf("%d%d",&n,&m);
a[1]=-inf,a[n+2]=inf;
for(int i=1;i<=n;i++){
a[i+1]=i;
}
root=build(1,n+2,0);
for(int i=1,l,r;i<=m;i++){
scanf("%d%d",&l,&r);
reverse(l+1,r+1);
}
getans(root);
return 0;
}
评论