这个算法还是比较容易理解的,只是代码调的我有点崩溃(还不是我太蒻了),因此学习笔记写的会比较简单。
本博客参考:PoPoQQQ 的课件;ChinHhh 的博客; attack 的代码启发。
前置
- 知识点:DFS序、线段树。
然后是一些概念:
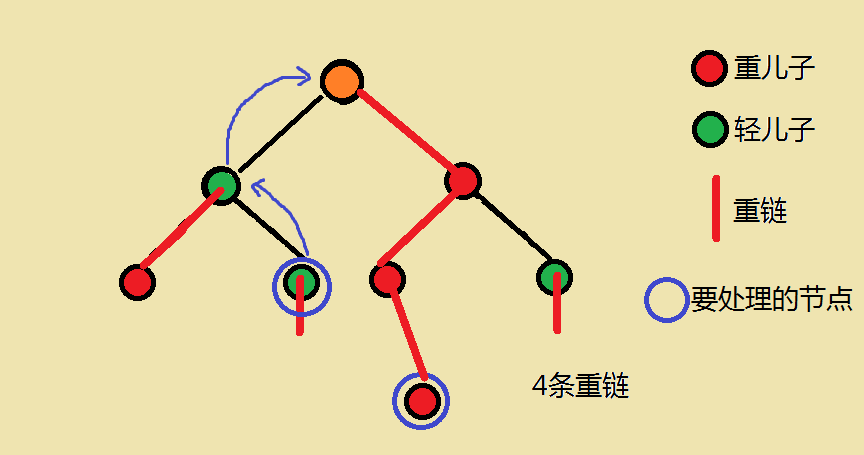
- 重儿子:一个节点的子节点中,$size$(即子树大小)最大的那个。;
- 轻儿子:非重儿子的子节点;
- 重边:一个点到它的重儿子的边;
- 轻边:一个点到它的轻儿子的边;
- 重链:由重边连结形成的链;
- 链顶:一条重链中深度最小的节点。
显然,一个非叶节点有且仅有一个重儿子。
树链剖分模板题:Luogu3384。
预处理
预处理主要是两遍 dfs。
dfs1
第一次 dfs 处理出每个点和深度/父亲/子树大小/重儿子。
inline void dfs1(int u,int f,int depth){
dep[u]=depth;//深度
fa[u]=f;siz[u]=1;//父亲
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(v==f) continue;
dfs1(v,u,depth+1);
siz[u]+=siz[v];//子树大小
if(siz[v]>siz[son[u]]) son[u]=v;//重儿子
}
}
dfs2
第二次 dfs 处理出 dfs 序(注意,这个 dfs 序是在先走重儿子前提下建立的 dfs 序)并把树上点的值赋到对应的新编号上,同时处理每个点所在链的链顶。
inline void dfs2(int u,int Top){
id[u]=++tot;//记录在 dfs 序中新编号
a[tot]=v[u];//赋值
top[u]=Top;//处理链顶
if(!son[u]) return;
dfs2(son[u],Top);//先走重儿子,Top 不变
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(v==fa[u]||v==son[u]) continue;
dfs2(v,v);//轻儿子的链顶变成他自己
}
}
容易发现两个性质:
- 每一条重链的编号是连续的;
- 每一棵子树的编号是连续的。
这两个性质是我们处理问题的关键。
建树
就是把新编号形成的新序列建成线段树,与正常线段树建树相同,不多阐述,可见文末完整代码。
简单问题的处理
树链剖分实际上就是把树上的问题转到新的依照 dfs 序形成的序列中进行处理,因而这里介绍模板题中四个问题的处理,即处理一段路径或是处理一棵子树。处理方法可以在不同题目间转化/引申。
求两点路径上的点权和
求两点路径上的点权和时,我们假定点 $x$ 为链顶更深的那个点,那我们每次都将 $ans$ 加上 $x$ 点至其链顶的点权和,然后再将他跳到其链顶上面一个点。我们反复执行这个步骤,直至两点在同一条链上,直接求出区间和即可。
线段树模板就略去了,有需要的可以在文末给出的代码中查看。
inline void queryTree(int x,int y){
int ret=0;
while(top[x]!=top[y]){//跳到处于同一条链上为止
if(dep[top[x]]<dep[top[y]]) swap(x,y);//跳链顶深的那个点
ret+=query(1,1,n,id[top[x]],id[x]);//转到线段树
ret%=mod;
x=fa[top[x]];
}
if(dep[x]>dep[y]) swap(x,y);
ret+=query(1,1,n,id[x],id[y]);//转到线段树
ret%=mod;
printf("%d\n",ret);
}
将两点路径上的点权都加上一个值
处理方法同上,直接给出代码。
inline void addTree(int x,int y,int k){
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]) swap(x,y);
add(1,1,n,id[top[x]],id[x],k);//转到线段树
x=fa[top[x]];
}
if(dep[x]>dep[y]) swap(x,y);
add(1,1,n,id[x],id[y],k);//转到线段树
}
求子树的点权和
由于子树内编号是连续的,且我们记录了子树大小,这个问题就非常容易处理了。
scanf("%d",&x);
printf("%d\n",query(1,1,n,id[x],id[x]+siz[x]-1));//直接转为线段树上求区间和
子树的点权都加上一个值
处理方法同上,直接给出代码。
scanf("%d%d",&x,&z);z%=mod;
add(1,1,n,id[x],id[x]+siz[x]-1,z);//直接转为线段树上区间加
总结 & 一道练手题
简单总结一下树剖的步骤:
- 根据题目需要写出线段树处理问题的代码;
- 两边 dfs ,然后建树;
- 再把问题需要处理的树上路径转化成线段树上的区间。
Luogu1505 [国家集训队]旅游 主要是码量不小,练手挺好,有一个简单的知识点,就是将边权转化为点权,也比较容易。
复杂度证明
树链剖分的复杂度为 $O(n\log^2n)$。
简单说,就是每次询问,树上跳来跳去需要一个 $\log$,然后线段树查询需要一个 $\log$。
线段树查询的复杂度这个不谈,稍微证明一下为什么树上最多跳 $O(\log n)$ 次。
容易想到,我们只需要证明任意一点到根的路径上有不超过 $O(\log n)$ 条重链,由于轻重链交错,所以只需要证明有不超过 $O(\log n)$ 条轻边即可。
于是:任意一点 $x$ 沿着父亲往上走,如果走过一条轻边,因为这是轻边,所以父亲一定有个重儿子比当前儿子大,也就是说 $size_{fa[x]}>size_x\times2$,因此,显然有走到根节点最多走的轻边不超过 $O(\log n)$ 条。
完整代码(Luogu3384 【模板】轻重链剖分)
#include<bits/stdc++.h>
#define ls u<<1
#define rs u<<1|1
using namespace std;
const int N=2e5+5;
struct SegmentTree{
int len,tag,sum;
}tree[N<<3];
struct edge{
int to,nxt;
}e[N<<1];
int cnt,head[N],n,m,mod,r;
int v[N],a[N];
inline void add(int u,int v){
e[++cnt].to=v;
e[cnt].nxt=head[u];
head[u]=cnt;
}
int dep[N],fa[N],son[N],siz[N],top[N],id[N];
inline void dfs1(int u,int f,int depth){
dep[u]=depth;
fa[u]=f;siz[u]=1;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(v==f) continue;
dfs1(v,u,depth+1);
siz[u]+=siz[v];
if(siz[v]>siz[son[u]]) son[u]=v;
}
}
int tot;
inline void dfs2(int u,int Top){
id[u]=++tot;
a[tot]=v[u];
top[u]=Top;
if(!son[u]) return;
dfs2(son[u],Top);
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(v==fa[u]||v==son[u]) continue;
dfs2(v,v);
}
}
inline void pushdown(int u){
if(!tree[u].tag) return;
tree[ls].tag=(tree[ls].tag+tree[u].tag)%mod;
tree[rs].tag=(tree[rs].tag+tree[u].tag)%mod;
tree[ls].sum=(tree[ls].sum+tree[ls].len*tree[u].tag)%mod;
tree[rs].sum=(tree[rs].sum+tree[rs].len*tree[u].tag)%mod;
tree[u].tag=0;
}
inline void pushup(int u){
tree[u].sum=(tree[ls].sum+tree[rs].sum)%mod;
}
inline void build(int u,int l,int r){
tree[u].len=r-l+1;
if(l==r){
tree[u].sum=a[l];
return;
}
int mid=(l+r)>>1;
build(ls,l,mid);
build(rs,mid+1,r);
pushup(u);
}
inline void add(int u,int l,int r,int L,int R,int k){
if(l>R||r<L) return;
if(l>=L&&r<=R){
tree[u].sum+=tree[u].len*k;
tree[u].tag+=k;
return;
}
pushdown(u);
int mid=(l+r)>>1;
add(ls,l,mid,L,R,k);
add(rs,mid+1,r,L,R,k);
pushup(u);
}
inline int query(int u,int l,int r,int L,int R){
if(l>R||r<L) return 0;
if(l>=L&&r<=R) return tree[u].sum;
pushdown(u);
int ret=0;
int mid=(l+r)>>1;
ret+=query(ls,l,mid,L,R);
ret+=query(rs,mid+1,r,L,R);
ret%=mod;
return ret;
}
inline void addTree(int x,int y,int k){
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]) swap(x,y);
add(1,1,n,id[top[x]],id[x],k);
x=fa[top[x]];
}
if(dep[x]>dep[y]) swap(x,y);
add(1,1,n,id[x],id[y],k);
}
inline void queryTree(int x,int y){
int ret=0;
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]) swap(x,y);
ret+=query(1,1,n,id[top[x]],id[x]);
ret%=mod;
x=fa[top[x]];
}
if(dep[x]>dep[y]) swap(x,y);
ret+=query(1,1,n,id[x],id[y]);
ret%=mod;
printf("%d\n",ret);
}
int main(){
scanf("%d%d%d%d",&n,&m,&r,&mod);
for(int i=1;i<=n;i++) scanf("%d",&v[i]);
for(int i=1,u,v;i<n;i++){
scanf("%d%d",&u,&v);
add(u,v);add(v,u);
}
dfs1(r,0,1);
dfs2(r,r);
build(1,1,n);
while(m--){
int opt,x,y,z;
scanf("%d",&opt);
if(opt==1){
scanf("%d%d%d",&x,&y,&z);
z%=mod;
addTree(x,y,z);
}
else if(opt==2){
scanf("%d%d",&x,&y);
queryTree(x,y);
}
else if(opt==3){
scanf("%d%d",&x,&z);z%=mod;
add(1,1,n,id[x],id[x]+siz[x]-1,z);
}
else{
scanf("%d",&x);
printf("%d\n",query(1,1,n,id[x],id[x]+siz[x]-1));
}
}
return 0;
}
评论