博客参考:CSDN 的 文章, enceladus, yybyyb, hyfhaha 的代码启示,皎月半洒花 的 博客, hyfhaha 的 博客。
前置知识 I – KMP字符串匹配
模版:Luogu3375。
我觉得这玩意儿比 trie 树难理解一点。
给定两个字符串 $s_1$ 和 $s_2$,我们需要求出 $s_2$ 在 $s_1$ 中所有出现的位置。
border:我们定义字符串 $s$ 的 border 为一个非 $s$ 本身的子串 $t$,满足 $t$ 既是 $s$ 的前缀,又是 $s$ 的后缀。
例如:ababab 的 border 有ab, abab,其中最长 border 为 abab。
我们先假定我们求出了 $s_2$ 所有前缀的最长 border。
我们考虑一组样例:
s1:abcabdababcabc
s2:abcabc
首先,我们一位一位进行匹配,容易发现前 $5$ 位都能匹配成功,而第 $6$ 位匹配失败了。在朴素情况下,这时候我们会从 $s_1$ 的第 $2$ 位开始再尝试一次匹配,但求出了最长 border 以后,这样做显然是愚蠢的。我们得知 $s_2$ 的前 $5$ 位的最长 border 为 ab。由 border 的定义可以得知,我们可以将 $s_2$ 前 $5$ 位中的最前两位(即第一二位)移到 $s_2$ 前 $5$ 位中原来最后两位的位置(即第四五位),也就是说:
s1:abcabdababcabc
s2: abcabc
然后再尝试匹配。由于 ab 是最长 border,因此我们如果从第二三位开始匹配一定是失败的,否则最长 border 就不是 ab 了。
理由:前 $5$ 位已经匹配成功了,如果我们把 $s_2$ 的头移到第 $2$ 位还能成功,那么 $s_2$ 的前 $4$ 位与 $s_2$ 的 $2 \sim 5$ 位一定的相同的,最长 border 的长度自然也不会是 $2$ 了。
以此类推,如果再次匹配失败,我们再去找前 $2$ 位的最长 border ,直至最长 border 的长度为 $0$(在此样例中,第二次就找不到了)。
我们记 $s_2$ 的长度为 $i$ 的前缀的最长 border 的长度为 $kmp_i$,那么我们可以写出如下代码:
j=0;
for(int i=1;i<=la;i++){
while(j&&b[j+1]!=a[i]) j=kmp[j];//s2 的第 j+1 位匹配失败,回到第 kmpj+1 位匹配看看
if(b[j+1]==a[i]) j++;//a 数组为 s1,b 数组为 s2
if(j==lb){//lb 为 s2 的长度
printf("%d\n",i-lb+1);//输出位置
j=kmp[j];//匹配成功后回到第 kmpj 位,接着匹配
}
}
接着我们考虑如何求 $kmp$ 数组。
我们尝试将 $s_2$ 和自己进行一次 kmp 匹配。首先我们发现以第一位开头一定能匹配成功(就是他自己嘛)。然后我们从第 $2$ 位开始 kmp 匹配,我们发现到第 $i$ 位时,当前还能够成功匹配的位数就是 $kmp_i$,理由如下:

当我们匹配到第 $i$ 位时,我们发现当前能和 $j$ 位匹配成功(即图中橙色部分),由于是和自己进行 kmp 匹配,也就是说 $s_1$ 和 $s_2$ 实质相同,那么我们就发现对于这个字符串的长度为 $i$ 的前缀,它的前 $j$ 位和末 $j$ 位是相同的,也就说,$kmp_i=j$。
至于为什么是最长的,这个很显然,你都进行 kmp 匹配了,如果有更长的可行的话,你在更长的时候肯定就已经停下来了,所以我们更新 $kmp$ 时的 $j$ 一定是可行的最长的 $j$。
j=0;
for(int i=2;i<=lb;i++){
while(j&&b[i]!=b[j+1]) j=kmp[j];//由于 j 一定比 i 小且显然 kmp[1]=0,所以这一步时所用到的 kmp[j] 肯定时早就求好了的,不用担心出问题
if(b[i]==b[j+1]) j++;//能匹配,就匹配
kmp[i]=j; //更新 kmp
}
至此, KMP字符串匹配,over(写得真长啊)!
前置知识 II – Trie 树
Trie 树,也称字典树/前缀树。是一种处理字符串匹配的数据结构。
这玩意儿速度是真不错,但是耗内存也是真大
假设有 $6$ 个字符串:cod,code,cook,five,file,fat,那么他们构造成的 Trie 树就是这样的:
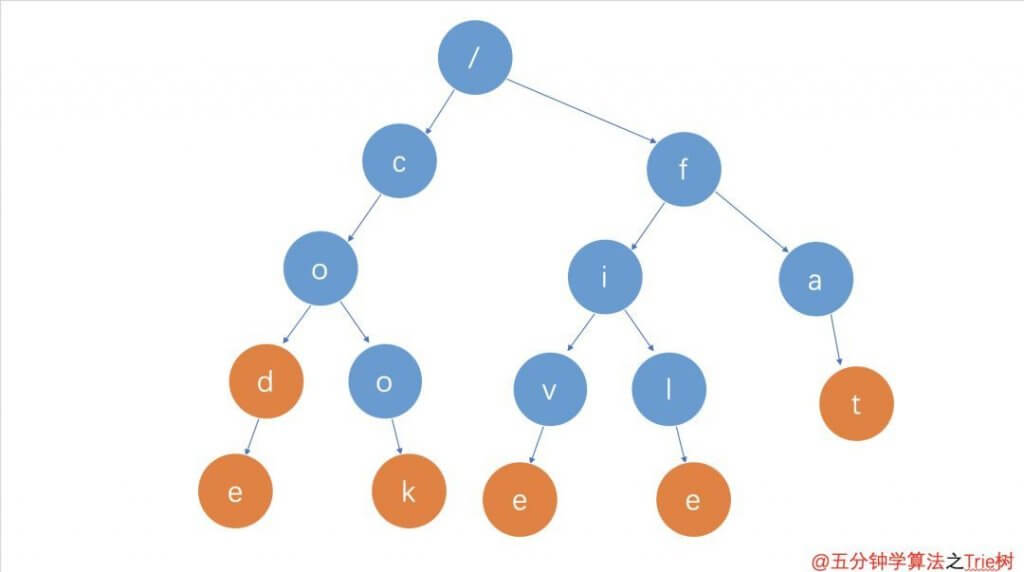
上图中,橙色结点为关键点。
容易发现 Trie 树的特性:
- 根节点不包含字符,其余结点各包含一个字符
- 从根节点到关键点路径上经过的字符连起来就是一个所需要的字符串
- 所有节点的子节点的字符互不相同
查询时,只要从根节点开始逐层匹配,搜寻下一层有无需要的字符,如没有,则说明所查询的字符串不存在。
一道例题:Luogu3879 [TJOI2010]阅读理解。
结合这题来讲述 trie 树的代码。
插入
inline void insert(int k){//k 表示第 k 个句子,见题面
scanf("%s",ch+1);
int len=strlen(ch+1);
int u=0;//从根节点开始
for(int i=1;i<=len;i++){
int x=ch[i]-'a';
if(!nxt[u][x]) nxt[u][x]=++tot;//看看下一层有没有所需的字符,没有就新建一个
u=nxt[u][x];//然后往下走
}
b[u][k]=1;//u 结点存在于第 k 个句子中,也就是以 u 为结尾的字符串存在于第 k 个句子中
}
查询
inline void check(){
scanf("%s",ch+1);
int len=strlen(ch+1);
int u=0;
bool flag=1;
for(int i=1;i<=len;i++){
int x=ch[i]-'a';
if(!nxt[u][x]){//下一层没有所需的字符,说明不存在
flag=0;break;
}
u=nxt[u][x];
}
if(flag){//如存在,输出其所在的字符串
for(int i=1;i<=n;i++)
if(b[u][i]) printf("%d ",i);
}
printf("\n");
}
前面说过 trie 树耗内存,所以这题 $b$ 数组必须要用 bitset 存,不然会 MLE。
trie 树比较容易理解,讲了这么多也就差不多了。
AC自动机
模版题:Luogu3808。
AC自动机,有人说就是在 Trie 上跑 kmp。对于这个说法且持保留意见,但AC自动机确实是以 Trie 树为基础的,且使用了 kmp 的思想。
以 Luogu3808 为例,对于这道题,我们先朴素地考虑这个问题:我们可以先建出一棵 Trie 树,然后在这棵 Trie 树上跑文本串。这时候我们需要考虑到一个问题,当我们跑到 Trie 树上的某一个点之后,如果发现跑不下去了(也就是说这个点的儿子没有文本串的下一个字符了)该怎么办。显然,如果我们再从根开始找的话是非常愚蠢的。这时候我们运用 kmp 的思想,从一个能接下去的地方接下去,而实现方式也就是AC自动机的核心——适配指针(即 fail 指针,以下常称 fail)。
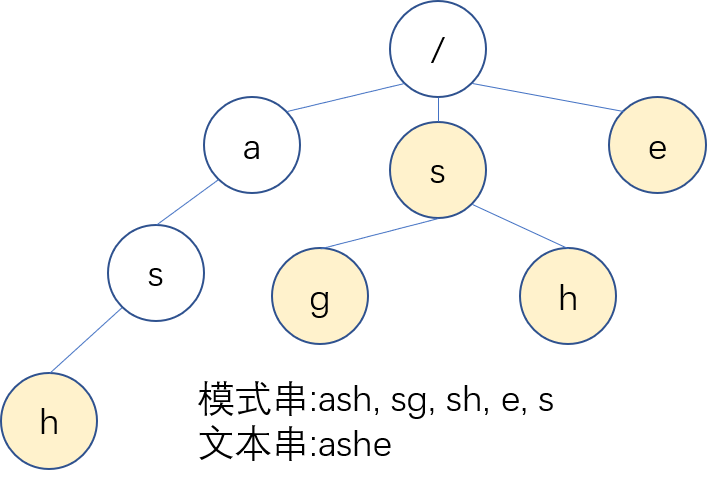
我们考虑这张图,我们在跑文本串时,一定会先走到 $a$ ,在走到 $a$ 的儿子的那个 $s$,这时我们发现,右边的那个 $s$ 理应被找到。因此,我们首先需要让这些能找到的点在我们跑 Trie 的其他子树时也可以链接起来。
我们考虑构造 fail ,fail 满足:如果一个点 $i$ 的 fail 指向 $j$。那么根到 $j$ 的字符串是根到 $i$ 的字符串的一个后缀。容易发现,深度为 $1$ 的点的 fail 指向根,一切节点的 fail 指向的点的深度都比当前点浅(否则他们就成了两个相同的串,在 Trie 中显然不会存在)。
下面结合代码来说明 fail 的构造方法:
inline void Get_Fail(){
queue<int> q;
for(int i=0;i<26;i++)
if(tree[0].to[i]!=0) q.push(tree[0].to[i]);
while(!q.empty()){
int u=q.front();
q.pop();
for(int i=0;i<26;i++){
if(tree[u].to[i]){
tree[tree[u].to[i]].fail=tree[tree[u].fail].to[i];
q.push(tree[u].to[i]);
}
else
tree[u].to[i]=tree[tree[u].fail].to[i];
}
}
}
由于一切节点的 fail 指向的点的深度都比当前点浅,我们可以采用 bfs,我们先把深度为 $1$ 的点推进队列里,然后对于每一个点遍历他的儿子,如果儿子存在的话,就把儿子的 fail 变成自己的 fail 的那个对应的儿子的点。如果儿子不存在,就用同样的方法找出一个可行的点作为自己的儿子(也就是方便文本串在走到走不下去时能正确跳转)。
可以尝试手玩代码(理解AC自动机的核心就在手玩和画图)。下面给出上图 fail 的构建结果。
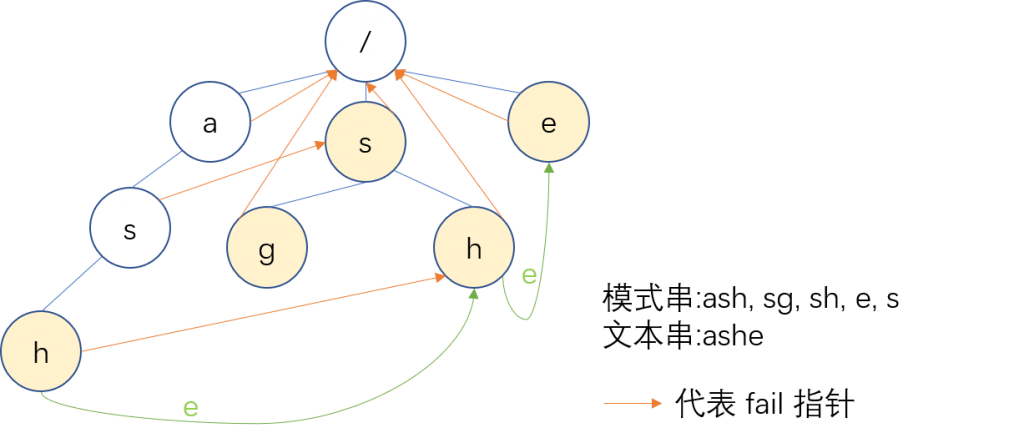
橙色的箭头表示 fail 指针,我们发现这样构建之后,我们在找到 ash 时也能够通过 fail 跳到 sh 的 $h$ 上,这样就不会漏过那个子串了。同时,我用绿色的箭头特以标注了 $e$ 这个字母的去向。再搜索到第二层时,我们发现第二层的 $h$ 没有 $e$ 这个儿子,那么他就将自己的 $e$ 儿子变成了自己的 fail 的 $e$ 儿子,也就是右边这个 $e$。再搜到第三层的 $h$ 时,他的 $e$ 儿子指向 fail 的 $e$ 儿子,也就是右边这个 $e$,这样子,我们就成功做到了在左边的 ash 搜完了之后AC自动机能自动跑到右边的 e 继续进行匹配。当然,如果整个 Trie 都找不到合适的字符,当前点就会乖乖地变成根(即 $0$ 号节点),然后从根继续开始搜索,也不会有问题。
理解了 fail 之后,我们就能比较容易地解决 Luogu3808 了,我们只需要先用 Trie 树插入每一个模式串并标记终点,然后构建出 fail,最后再用文本串跑一遍就好了,下面给出询问答案(query)的代码。
inline void query(){
scanf("%s",s);
int u=0,ans=0;
int l=strlen(s);
for(int i=0;i<l;i++){
u=tree[u].to[s[i]-'a'];//前面都构筑好了,所以直接走到下一个就好了
for(int t=u;t&&(!vis[t]);t=tree[t].fail){//通过 fail 确保没有漏的子串
ans+=tree[t].ans;
vis[t]=1;
}
}
printf("%d\n",ans);
}
一种AC自动机的优化
前置:Luogu3796。
首先你需要做掉前置,其实非常容易,只需要记录一下每一个编号的子串对应的终点,然后对询问做出一点变更:
inline void query(string s){
int l=s.length();
int u=0;
for(int i=0;i<l;i++){
u=tree[u].to[s[i]-'a'];
for(int t=u;t;t=tree[t].fail) ans[t].cnt++;//由于我们需要统计每一个子串的出现次数,
}//所以同一个子串可能会被统计好多次,也就是说每一个终点都可能会用到多次,我们就不能用 vis 数组了,
}//一定要每一次都跳一遍所有 fail
然后我们容易发现,这个代码由于没有 vis 数组,所以复杂度假掉了(容易发现,对于一个 aaaaa__aaaaa 的串,会很容易被卡掉)。那么对于这个模板题 Luogu5357, 我们使用这个代码就会 TLE,因此我们需要考虑优化。
在 Luogu3808 中,我们利用 vis 数组保证了 Trie 树的所有点最后只被走一遍,那么对于这个我们有没有办法做到这一点呢?显然是有的,我们可以在询问时不暴力跳 fail,而是简单地将这一点答案 $+1$ 就可以了。因为我们发现如果将 fail 看作连边,Trie 树显然形成了一张 DAG,我们只需要最后跑一遍拓扑将答案更新一下就可以了。这样我们暴力跳的无数次 fail 就又变成了只跳一次,只是跳的这一次更新的答案也不是 $1$ 而是很多而已。个人觉得不难理解,下面给出部分代码,可以结合代码加深理解。
inline void Get_Fail(){
queue<int> q;
for(int i=0;i<26;i++)
if(tree[0].to[i]) q.push(tree[0].to[i]);
while(!q.empty()){
int u=q.front();q.pop();
for(int i=0;i<26;i++){
if(tree[u].to[i]){
tree[tree[u].to[i]].fail=tree[tree[u].fail].to[i];
in[tree[tree[u].to[i]].fail]++;//建拓扑图,边就是 fail,已经连好了,因此无需额外写一个数组保存边
q.push(tree[u].to[i]);
}
else tree[u].to[i]=tree[tree[u].fail].to[i];
}
}
}
inline void query(string s){
int l=s.length();
int u=0;
for(int i=0;i<l;i++){
u=tree[u].to[s[i]-'a'];
tree[u].ans++;//只需 ans++,无需跳 fail
}
}
inline void topu(){//在 query 之后紧接着就执行 topu
queue<int> q;
for(int i=0;i<=tot;i++) if(in[i]==0) q.push(i);
while(!q.empty()){
int u=q.front();q.pop();
in[tree[u].fail]--;
tree[tree[u].fail].ans+=tree[u].ans;//非常简单地传递答案即可。非关键点有 ans 值也是没有关系的,因为你在输出时根本就不可能用到这些点。
if(!in[tree[u].fail]) q.push(tree[u].fail);
}
}
完整代码
Luogu3808 【模板】AC自动机(简单版)
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5;
int n;
char s[N];
struct Trie_tree{
int fail,ans,to[26];
}tree[N<<3];
int cnt;
inline void insert(){
scanf("%s",s);
int l=strlen(s);
int u=0;
for(int i=0;i<l;i++){
if(!tree[u].to[s[i]-'a']) tree[u].to[s[i]-'a']=++cnt;
u=tree[u].to[s[i]-'a'];
}
tree[u].ans++;
}
inline void Get_Fail(){
queue<int> q;
for(int i=0;i<26;i++)
if(tree[0].to[i]!=0) q.push(tree[0].to[i]);
while(!q.empty()){
int u=q.front();
q.pop();
for(int i=0;i<26;i++){
if(tree[u].to[i]){
tree[tree[u].to[i]].fail=tree[tree[u].fail].to[i];
q.push(tree[u].to[i]);
}
else
tree[u].to[i]=tree[tree[u].fail].to[i];
}
}
}
bool vis[N<<3];
inline void query(){
scanf("%s",s);
int u=0,ans=0;
int l=strlen(s);
for(int i=0;i<l;i++){
u=tree[u].to[s[i]-'a'];
for(int t=u;t&&(!vis[t]);t=tree[t].fail){
ans+=tree[t].ans;
vis[t]=1;
}
}
printf("%d\n",ans);
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++) insert();
Get_Fail();
query();
return 0;
}
Luogu5357 【模板】AC自动机(二次加强版)
#include<bits/stdc++.h>
using namespace std;
const int N=2e6+5;
struct Trie_Tree{
int fail,to[26],ans;
}tree[N];
int match[N];
string S;
int tot,in[N];
inline void insert(string s,int k){
int l=s.length();
int u=0;
for(int i=0;i<l;i++){
if(!tree[u].to[s[i]-'a']){
tree[u].to[s[i]-'a']=++tot;
}
u=tree[u].to[s[i]-'a'];
}
match[k]=u;
}
inline void Get_Fail(){
queue<int> q;
for(int i=0;i<26;i++)
if(tree[0].to[i]) q.push(tree[0].to[i]);
while(!q.empty()){
int u=q.front();q.pop();
for(int i=0;i<26;i++){
if(tree[u].to[i]){
tree[tree[u].to[i]].fail=tree[tree[u].fail].to[i];
in[tree[tree[u].to[i]].fail]++;
q.push(tree[u].to[i]);
}
else tree[u].to[i]=tree[tree[u].fail].to[i];
}
}
}
inline void query(string s){
int l=s.length();
int u=0;
for(int i=0;i<l;i++){
u=tree[u].to[s[i]-'a'];
tree[u].ans++;
}
}
inline void topu(){
queue<int> q;
for(int i=0;i<=tot;i++) if(in[i]==0) q.push(i);
while(!q.empty()){
int u=q.front();q.pop();
in[tree[u].fail]--;
tree[tree[u].fail].ans+=tree[u].ans;
if(!in[tree[u].fail]) q.push(tree[u].fail);
}
}
int n;
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
cin>>S;
insert(S,i);
}
Get_Fail();
cin>>S;
query(S);topu();
for(int i=1;i<=n;i++)
printf("%d\n",tree[match[i]].ans);
return 0;
}
评论