题意
题目链接。
给定一张有向无自环图,求一个点集满足:
- 点集内任意两个不同点距离不小于 $2$(即无边相连)。
- 对于任意一个不在点集内的点,存在一个点集内的点到它的距离不大于 $2$(即两步能达)。
解析
算法实现与 @Mickey_snow、@_Anchor 等题解类似,本篇题解主要重申一种可能更清晰的证明以及错解的 Hack。
简单阐述解法:
- 先按序号从小到大循环,依次选中没有被标记的点,并将其所能一步到达且序号比其大的点都打上标记。
- 再按序号从大到小循环,同样选中没有被标记的点,并将其所能一步到达的点都打上标记。
- 仍未被打上标记的点即为答案点集。
证明
根据题意中的两个条件,证明也分为两部分。我们记“点集内任意两个不同点距离不小于 $2$(即无边相连)”为条件 1,记“对于任意一个不在点集内的点,存在一个点集内的点到它的距离不大于 $2$(即两步能达)”为条件 2。
条件 1 证明:
记点 $u$ 可以一步到达 $v$ 为 $u \rightarrow v$,记最终得到的点集为 $S$。
- 由解法的第一步可知,$S$ 中不存在 $u\rightarrow v$ 且 $u<v$,因为点 $v$ 肯定在遍历到 $u$ 就被打上标记了。
- 由解法的第二步可知,$S$ 中不存在 $u\rightarrow v$ 且 $u>v$,因为点 $v$ 肯定在遍历到 $u$ 就被打上标记了。
- 综上,$S$ 中不存在 $u\rightarrow v$。
条件 2 证明:
记解法第一步中被打上标记的点为 $S_1$,第二步中被打上标记的点为 $S_2$,最终得到的点集为 $S$。
- 由解法的第二步可知,对于 $S_2$ 中任意一点 $v$,存在 $S$ 中一点 $u$ 可一步到达 $v$。
- 由解法的第一步可知,对于 $S_1$ 中任意一点 $v$,存在 $S$ 或 $S_2$ 中一点 $u$ 可一步到达 $v$。
- 综上,对于 $S_1$ 中任意一点 $v$,存在 $S$ 中一点 $u$ 可一步或两步到达 $v$。
- 综合 1、3,对于 $S_1$ 或 $S_2$ 中任意一点 $v$,存在 $S$ 中一点 $u$ 可一步或两步到达 $v$,得证。
代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5;
struct node{
int to,nxt;
}e[N];
int head[N],cnt,ans,n,m;
inline void add(int u,int v){
e[++cnt].to=v;
e[cnt].nxt=head[u];
head[u]=cnt;
}
bool vis[N];
int main(){
scanf("%d%d",&n,&m);
for(int i=1,u,v;i<=m;i++){
scanf("%d%d",&u,&v);
add(u,v);
}
for(int u=1;u<=n;u++){//第一步
if(!vis[u]){
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(v>u) vis[v]=1;//只标记比它大的
}
}
}
for(int u=n;u>=1;u--){//第二步
if(!vis[u]){
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
vis[v]=1;//不需要判定,因为不可能出现小的标记大的(第一步中已执行)。
}
}
}
for(int i=1;i<=n;i++) if(!vis[i]) ans++;
printf("%d\n",ans);
for(int i=1;i<=n;i++) if(!vis[i]) printf("%d ",i);
return 0;
}
可能的错解
可能有人会有疑惑,为什么第一步中要规定只标记序号比它大的?能否去掉第一步中的 if(u>v) 这段代码呢(同时你还发现第二步就无意义了,甚至可以去除)?但是很遗憾,这是错误的。下面先给出一组 Hack 数据。
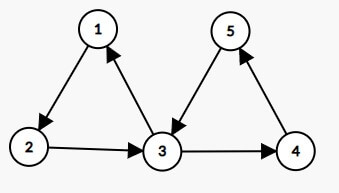
在错解的第一步中,点 $1$ 会给点 $2$ 打上标记,点 $3$ 会给点 $1,4$ 打上标记,点 $5$ 会给点 $3$ 打上标记,最终就只剩下了点 $5$ 显然不符合题意。
而我们再看正解,第一步中,点 $1$ 会给点 $2$ 打上标记,点 $3$ 会给点 $4$ 打上标记。第二步中,点 $5$ 会给点 $3$ 打上标记,然后点 $3$ 就不会再遍历了,因此点 $1$ 仍然存在,答案为 $1,5$ 是正确的。
于是错解的错误就显然了,对于那些在第二步中被标记的点,实际上它是不会给其他点打标记的,而在错解中却让它们进行了打标记操作,从而导致误伤了不该被去除的点。
至此,本题的解法与错解都说明完毕。