题意

题目链接

大体见翻译。注意树被”拍扁”到平面中之后，要求所有边都与坐标轴平行，且所有点是整点。

解析

首先有一件很显然的事情，就是如果有任意一个点的度数大于 $4$，结果一定为 $-1$，因为由于边的方向只有上下左右四种，所有第五条边是无论如何也无法连出去的。

接着考虑对于可行的情况，我们只需要满足没有任何两条边相交就可以了。那么我们考虑什么情况下边会发生相交。

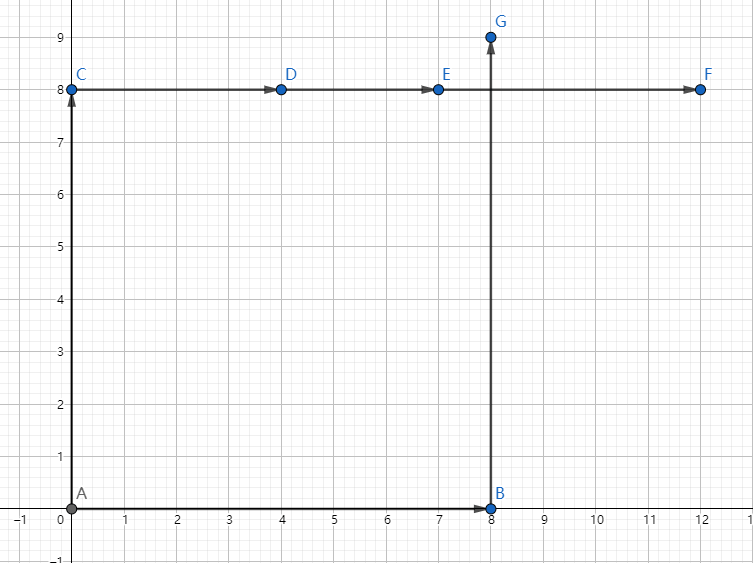
观察上图，我们发现，发生了相交的情况，以上图为例，就意味着 $CD+DE+EF>AB$ 且 $BG>AC$。

那么我们如何避免这种情况的出现呢？我们发现 $n$ 的范围只有 $30$，从而我们想到一个式子：

$$2^k>2^{k-1}+2^{k-2}…+2^1+2^0$$

因此我们可以在进行 dfs 绘点时，每次向下传递时都让 $k$ 减一，这样，上图中的 $CD+DE+EF$ 或是 $BG$ 最大（全满）时也仅能是 $AB-1$。

然后在 dfs 里还需要注意一点，就是不能往“来”时的方向，即父亲的方向走，记录一下即可。

代码

#include<bits/stdc++.h>
#define int long long 
using namespace std;
const int N=55;
int n,du[N];
struct edge{
    int to,next;
}e[N<<1];
int head[N],cnt,ansx[N],ansy[N];
int pos[4][2]={{1,0},{0,1},{-1,0},{0,-1}};
inline void add(int u,int v){
    e[++cnt].to=v;
    e[cnt].next=head[u];
    head[u]=cnt;
}
inline void dfs(int u,int f,int x,int y,int tag,int from){
    //tag 代表题解中的 k，from 代表父亲所在的方向 
    int tot=0;//tot 表示当前即将要走的方向 
    ansx[u]=x,ansy[u]=y;
    for(int i=head[u];i;i=e[i].next){
        int v=e[i].to;
        if(v==f) continue;
        if(tot==from) tot++;
        dfs(v,u,x+(1<<tag)*pos[tot][0],y+(1<<tag)*pos[tot][1],tag-1,(tot+2)%4);
        tot++;
    } 
}
signed main(){
    scanf("%lld",&n);
    for(int i=1,u,v;i<n;i++){
        scanf("%lld%lld",&u,&v);
        add(u,v);add(v,u);
        du[u]++;du[v]++;
        if(du[u]>4||du[v]>4){//度数超 4 
            printf("NO");
            return 0;
        }
    }
    dfs(1,0,0,0,30,-1);//这个 30 实际上也可以大一点 
    printf("YES\n");
    for(int i=1;i<=n;i++){
        printf("%lld %lld\n",ansx[i],ansy[i]);
    }
    return 0;
}