题目链接。
发现题解区说大多都是直接说再连一条边权为 $-1$ 的边,在这里略微证明一下正确性。
解析
首先发现若图中没有环,最大答案为所有联通块的最长链长度之和,最小答案为 $3$。
若存在环,则最大答案为所有环的 $\gcd$。为了在可接受的时间内找到所有环,我们对于每一条边的 $u\rightarrow v$,从 $u$ 向 $v$ 连一条边权为 $1$ 的边,从 $v$ 向 $u$ 连一条边权为 $-1$ 的边。然后每一次都从任意一个未被搜索过的点开始搜,并记录每一个点的距离 $dis$,若走到一个已走过的点 $i$,就取 $d-dis_i$ 作为一个新找到的环的长度,这部分代码如下:
inline void dfs(int u,int d){
if(dis[u]){
ans=gcd(ans,abs(d-dis[u]));
return;
}
dis[u]=d;vis[u]=1;
mx=max(mx,dis[u]);mn=min(mn,dis[u]);
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;dfs(v,d+e[i].w);
}
}
接着我们观察下面这张图。
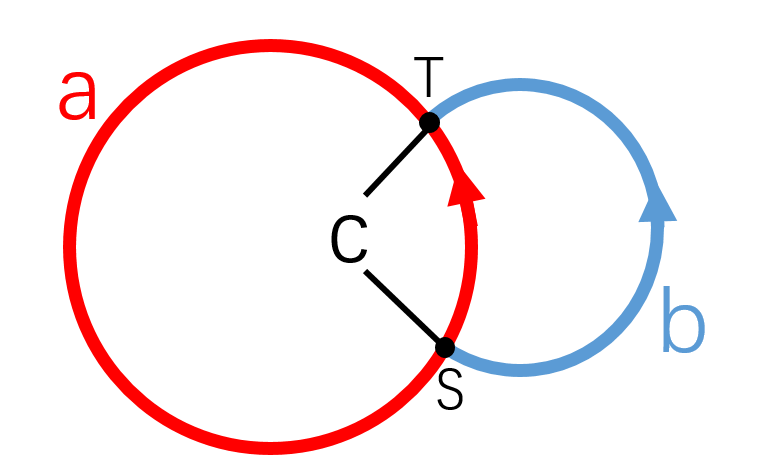
我们发现,当图中出现上图这个情况时,记 $a$ 为红色环的长度,$b$ 为蓝色部分的长度,$c$ 为中间部分的长度。这时的两个环的长度分别为 $a$ 和 $a+b-c$,但是我们搜索时搜出来的长度可能是 $a$ 和 $c-b$ 或 $a+b-c$ 和 $c-b$,即先搜完 $a$ 这个环,再从 $T$ 点以 $-1$ 的道路通过 $b$ 回到 $S$ 点。
也就是说,这个做法想要正确,需要有 $\gcd(a,a+b-c)=\gcd(a,|c-b|)$ 且 $\gcd(a,a+b-c)=\gcd(a+b-c,|c-b|)$。
先证明前者:
- 若 $b \ge c$,有 $\gcd(a,|c-b|)=\gcd(a,b-c)=\gcd(a,a+b-c)$,显然正确
- 若 $b<c$ ,有 $\gcd(a,|c-b|)=\gcd(a,c-b)=\gcd(a,a+c-b)$,换言之,我们需要证明 $\gcd(a,a+b)=\gcd(a,a-b),a>b$。
证明:
记 $x=\gcd(a,a-b)$,则 $x|a$ 且 $x|b$。
设 $a=mx$,$b=nx$,有 $m$ 与 $m-n$ 互质且 $m>n$,故 $\gcd(a,a+b)=\gcd(mx,(m+n)x)$。
若 $m+n$ 与 $m$ 不互质,有 $\gcd(m+n,m)=\gcd(n,m)\ne 1$。
可设 $t=\gcd(m,n)$,有 $m=k_1t,n=k_2t,m-n=(k_1-k_2)t$,与 $m$ 与 $m-n$ 互质矛盾。
故 $m+n$ 与 $m$ 互质,即 $\gcd(a,a+b)=x=\gcd(a,a-b)$。
再证明后者:
- 若 $c \ge b$,有 $\gcd(a+b-c,|c-b|)=\gcd(a+b-c,c-b)=\gcd(a+b-c,a)$。
- 若 $c<b$,有 $\gcd(a+b-c,|c-b|)=\gcd(a+b-c,b-c)=\gcd(a+b-c,a+2b-2c)$,将 $a+b-c$ 和 $b-c$ 分别看作 $\gcd(a,a+b)=\gcd(a,a-b)$ 中的 $a$ 和 $b$,由上得证。
同时我们又发现,除了上图的情况,其他的情况搜到的环的长度都是真是的或是可以化成上图情况的。
因此,建反向的边权为 $-1$ 的边的做法是正确的。求出最大答案后,最小答案显然为最大答案的最小的 $\ge3$ 的因子,求出答案后再判断一下和 $3$ 的关系即可。
代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
const int M=1e6+5;
int n,m;
struct node{
int to,nxt,w;
}e[M];
int cnt,head[N];
inline void add(int u,int v,int w){
e[++cnt].to=v;
e[cnt].nxt=head[u];
e[cnt].w=w;
head[u]=cnt;
}
int dis[N],ans,ans2,mx,mn;
bool vis[N];
inline int gcd(int a,int b){
return b==0?a:gcd(b,a%b);
}
inline void dfs(int u,int d){
if(dis[u]){
ans=gcd(ans,abs(d-dis[u]));
return;
}
dis[u]=d;vis[u]=1;
mx=max(mx,dis[u]);mn=min(mn,dis[u]);
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;dfs(v,d+e[i].w);
}
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1,u,v;i<=m;i++){
scanf("%d%d",&u,&v);
add(u,v,1);add(v,u,-1);
}
for(int i=1;i<=n;i++){
if(!vis[i]){
mx=-1e9;mn=1e9;
dfs(i,1);
ans2+=mx-mn+1;//找最长链
}
}
if(ans){//有环
if(ans<3) printf("-1 -1\n");
else for(int i=3;i<=ans;i++){
if(!(ans%i)){
printf("%d %d\n",ans,i);
return 0;
}
}
}
else{//没环
if(ans2<3) printf("-1 -1\n");
else printf("%d 3\n",ans2);
}
return 0;
}