题意

题目链接。

洛谷这题的评测似乎炸掉了，这里有 Znloye 提供的临时测试点。

求 $a^{a^{a^{\dots}}}(b\ 个\ a)$ 的末 $9$ 位数，$t$ 组数据。

解析

保留末 $9$ 位数等价于对于 $10^9$ 取模，再补全前边的 $0$ 即可。

而对于这种 Power Tower，一种常用的方法是使用扩展欧拉定理，再在快速幂上进行修改。

由扩展欧拉定理：

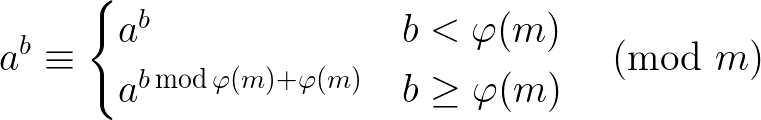
由于 $\varphi(m)$ 的下降速度是 $\log$ 级别的，因此我们可以进行暴力递归而不用担心复杂度。由于 $b\ge\varphi(m)$ 时我们还需要加上 $\varphi(m)$，因此需要对快速幂做一些修改。即有：

inline int ksm(int a,int b,int p){
    int ret=1;
    while(b){
        if(b&1){ret=ret*a;if(ret>=p) ret=ret%p+p;}
        a=a*a;if(a>=p) a=a%p+p;
        b>>=1;
    }
    return ret;
}

然后我们进行暴力递归，即有：

inline int solve(int x,int p){
    if(x==b+1||p==1) return 1;
    int y=solve(x+1,phi[p]);
    return ksm(a,y,p);
}

当 $x=b+1$ 或 $p=1$ 时返回 $1$，前者显然，后者时因为根据扩展欧拉定义，此时 $\varphi(m)=1$，故一定满足 $b\ge \varphi(m)$，返回值应该加上 $\varphi(m)$，即 $1$。

注意，如果最终答案大于 $10^9$ ，这样处理出来的最终答案也会被加上 $10^9$，因此我们在最终可以判断答案是否大于 $10^9$，若是则保留最后 $9$ 位，否则直接输出。

由于有用的 $\varphi(x)$ 的数量比较少，我们可以先预处理出来。

特别的，当 $a=0$ 的时候，由于该题中有 $0^0=1$，因此我们需要对于 $b$ 的奇偶进行特判，详见下边代码。

代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+5;
const int mod=1e9;
map<int,int> phi;
inline int getphi(int n){//求 phi
    int ret=n;
    for(int i=2;i*i<=n;i++){
        if(n%i==0){
            ret/=i;ret*=(i-1);
            while(!(n%i)) n/=i;
        }
    }
    if(n>1) ret/=n,ret*=(n-1);
    return ret;
}
inline int ksm(int a,int b,int p){//修改过的快速幂
    int ret=1;
    while(b){
        if(b&1){ret=ret*a;if(ret>=p) ret=ret%p+p;}
        a=a*a;if(a>=p) a=a%p+p;
        b>>=1;
    }
    return ret;
}
int T,a,b;
inline int solve(int x,int p){//核心的递归代码
    if(x==b+1||p==1) return 1;
    int y=solve(x+1,phi[p]);
    return ksm(a,y,p);
}
signed main(){
    int now=mod;
    while(now!=1) phi[now]=getphi(now),now=phi[now];
    phi[now]=1;
    scanf("%lld",&T);
    while(T--){
        scanf("%lld%lld",&a,&b);
        if(a==0){printf("%d\n",!(b&1));continue;}//特判
        int ans=solve(1,mod);
        if(ans<mod) printf("%lld\n",ans);//判断是否超过 9 位
        else{
            ans%=mod;
            int out[20],k=0;
            for(int i=1;i<=9;i++) out[i]=0;
            while(ans){
                out[++k]=ans%10;
                ans/=10;
            }//补零
            printf("...");
            for(int i=9;i>=1;i--) printf("%lld",out[i]);
            putchar('\n');
        }
    }
    return 0;
}

该题中所使用的方法实际还可以应用于很多类似的 Power Tower 题目。例如：CF906D Power Tower，P3934 [Ynoi2016] 炸脖龙 I ，P3747 [六省联考 2017] 相逢是问候。