区间信息维护
前缀和与差分
多维前缀和
多维前缀和可以通过一维一维处理的方式,将复杂度控制在可控范围。
例如二维前缀和求法:
- $sum_{i,j}=a_{i,j}$
- $sum_{i,j}+=sum_{i-1,j}$
- $sum_{i,j}+=sum_{i,j-1}$
数列上加多项式
给一个数列的一部分连续的数分别加上 $f(1),f(2),\dots,f(n),\dots$
key:任何一个最高次数为 $n$ 的多项式连续数列可以通过差分 $n+1$ 次表示。
因此,对于区间 $(l,r)$,我们先差分出一个从 $l$ 开始的 $f(1)$ 开始的数列,再差分出一个从 $r+1$ 开始的 $-f(r-l+2)$ 开始的数列抵消影响。
例题:NC225628 智乃酱的静态数组维护问题多项式。
树状数组与线段树
离线后树状数组
一些统计种类的问题可以通过这个方法来解决。
例如 [HEOI2012]采花
LazyTag
懒标记是线段树的核心之一。考虑需要维护的数值在懒标记下的运算很关键。
给出例题:
线段树
智乃酱的cube
带修改的 DP(DDP)
通过线段树可以完成一些能通过矩阵优化的 DP 的待修改版本。
智乃酱的双塔问题·极(带修改的DP,DDP)
智乃酱的双塔问题·改
势能线段树(带暴力成分的线段树)
有些数据具有单调性,就像势能不断下降至 0 势能点,观察并维护之可以让一些线段树结构看似有暴力修改,实则复杂度合法。
势能线段树模板题二
弩蚊怒夏
李超线段树
李超线段树是用来维护平面上的若干点的,用于快速找出在某一个 x 坐标,那一条的 y 值最大或最小。这在动态规划优化中也有作用。
模板:智乃的直线
平衡树
绝大部分时候,set 都可以解决问题,因此在比赛中非必要,不要贸然使用平衡树,平衡树在 ACM/ICPC 中并不是一个需要经常手写的数据结构。由于相较于 Treap,Splay 拥有更广泛的使用场合,因此此处只呈现 Splay 的代码。
[!Warning]
set中每个元素只能出现一次,遇到有重复数据的情况是不能使用的,需要使用multiset
平衡树管理数组的一个优势是他的区间长度是自由的,因此对于区间反转这一问题,线段树无法通过打 tag 来解决,而平衡树可以做到,这一类需要严格对某一个自由长度区间打 tag 的操作是平衡树之于线段树的优势。
我的博客中有对平衡树的详细学习笔记。
例题:
[HNOI2004]宠物收养所 请注意,本题可以通过 Set 解决,相较于手写平衡树,这是更优秀的选择。
普通平衡树 这是一道模板题
文艺平衡树 这是另一道模板题
跳表
首先,跳表是一种离线算法, 这是很重要的一点。
跳表(ST 表)有两种,一种是传统的 log 型跳表,建立复杂度为 $O(n\log n)$,但必须要满足所求的内容在区间重叠不影响结果(例如,gcd 或者 max/min)。
另一种是根号型跳表,记 $f_{i,j}$ 为从 $i$ 开始的 $j$ 个数的值(例如,和),记 $g_{i,j}$ 为从 $i$ 开始的 $block \times j$ 个数的和,通常我们令 $block=\operatorname{sqrt}(n)$。这样,我们可以在 $O(n \sqrt n)$ 的时间复杂度内建立跳表,然后在 $O(1)$ 的时间复杂度内进行单次查询(大块+小块)。请注意,只有当查询次数不小于数组总长的 $100$ 倍时才需要使用根号跳表,否则,线段树是一个更好的选择。不同于 log 型跳表,区间跳表只要满足区间可加性就能做(这与线段树的要求相同,不是吗)。
分块
对于一些问题,我们可以将整个区间分成 $\operatorname{sqrt}(n)$ 个块。如果我们可以记录每个块的总值,或是对无效的块打上标记,我们就可以保证每次查询的时间复杂度为 $O(\sqrt n)$。
莫队
普通莫队
普通莫队是一个离线算法。
我们先将整个区间分成 $\sqrt n$ 个块。对于所有查询 $[l,r]$,我们先根据 $l$ 所在的块进行升序排序,相同时再根据 $r$ 的大小进行升序排序。我们以这个顺序处理所有查询,对于一次查询,我们只需要访问上一次查询没有查询过的点,再删除该次查询没有但上一次查询有的点即可。时间复杂度为 $O(n\sqrt n)$。
例题:小Z的袜子
带修莫队
在普通莫队的前提下,如果题目有了单点修改的操作,我们就可以使用带修莫队。
待修莫队给了所有查询第三维时间戳,即代表这个查询经过了几次单点修改。对于所有查询 $[l,r,tim]$,我们先根据 $l$ 所在的块进行升序排序,相同时再根据 $r$ 所在的块进行升序排序,仍然相同则根据 $tim$ 的大小升序排序。请注意,再待修莫队中,块长为 $n^{\frac{2}{3}}$。最终时间复杂度为 $O(n^{\frac{3}{5}})$.
例题:数颜色
树上莫队
如果有一个问题和普通莫队要求的内容类似,但是查询的是树上一条链的结果,就可以用树上莫队。
首先,我们求出这棵树的欧拉序(即,一个点进出分别会被继续一次,记进的时间戳为 $in_u$,出的时间戳为 $out_u$)。对于一次询问 $[u,v]$,不妨令 $in_u \le in_v$,如果 $out_u \ge out_v$,即点 $v$ 是点 $u$ 子树上的点,则 $(u,v)$ 链上的点是欧拉序中 $[in_u,in_v]$ 区间内所有出现次数为奇数的点,否则 $(u,v)$ 链上的点是欧拉序中 $[out_u,in_v]$ 区间内所有出现次数为奇数的点,再加上 $\operatorname{lca}(u,v)$。如此以来,我们就把树上的问题转化成了区间查询,再利用普通莫队的方法即可,只是对数的加减改成了对某点出现次数奇偶性的更改,若为奇数,则加入该点,否则删除该点。令块长为 $\sqrt n$,则时间复杂度为 $O(n\sqrt n)$。
例题:树上莫队模板题
可并堆/左偏树
左偏树是一种堆的实现,他保证了对于任意一点,左链的长度始终大于右链,因此在合并过程中,只要我们一直考虑右链,即,若要合并的两个小根堆堆顶为 $x,y$,若 $x<y$ 就用 $x$ 的右儿子与 $y$ 继续合并,反之用 $y$ 的右儿子和 $x$ 继续合并,如此一来,就能保证合并的时间复杂度为 $O(\log n)$。
例题:【模板】左偏树/可并堆
笛卡尔树
笛卡尔树是一种中序遍历与数列相同,且具有堆结构的一种二叉树,可以把数列问题转化到树上问题。我们可以用一个单调栈来建立笛卡尔树,例如,对于一个大根堆的笛卡尔树,可以通过如下代码建立:
stack<int> st;
for(int i=1;i<=n;i++){
while(!st.empty()&&a[i]>a[st.top()]){ls[i]=st.top();st.pop();}
if(!st.empty()) rs[st.top()]=i;
st.push(i);
}
例题:Add One 2
代码
树状数组
#define lowbit(x) ((x)&(-x))
ll tr[N];
void add(int x,ll k){while(x<=n){tr[x]+=k;x+=lowbit(x);}}
ll query(int x){ll ret=0;while(x){ret+=tr[x];x-=lowbit(x);}return ret;}
线段树
struct SegmentTree{
#define ls ((u)<<1)
#define rs ((u)<<1|1)
struct node{
int l,r;
}tr[4*N];
void init_lazy(int u){
}
void union_lazy(int fa,int u){
}
void cal_lazy(int u){
}
void pushdown(int u){
if(){
cal_lazy(u);
if(tr[u].l!=tr[u].r){
union_lazy(u,ls);
union_lazy(u,rs);
}
init_lazy(u);
}
}
void pushup(int u){
pushdown(ls);pushdown(rs);
}
void build(int u,int l,int r,ll *A){
tr[u].l=l;tr[u].r=r;
init_lazy(u);
if(l==r){
}
else{
int mid=(l+r)>>1;
build(ls,l,mid,A);build(rs,mid+1,r,A);
pushup(u);
}
}
void change(int u,int L,int R,ll k,int opt){
pushdown(u);
if(tr[u].r<=R&&tr[u].l>=L){
tr[u].lazy[opt]=k;
return;
}
int mid=(tr[u].l+tr[u].r)/2;
if(R<=mid){change(ls,L,R,k,opt);}
else if(L>mid){change(rs,L,R,k,opt);}
else{change(ls,L,R,k,opt);change(rs,L,R,k,opt);}
pushup(u);
}
ll query(int u,int L,int R){
pushdown(u);
if(tr[u].r<=R&&tr[u].l>=L) return ;
int mid=(tr[u].l+tr[u].r)/2;
if(R<=mid) return query(ls,L,R);
else if(L>mid) return query(rs,L,R);
else return query(ls,L,R)+query(rs,L,R);
}
}ST;
李超线段树
struct Line{
ll k,b;
ll val(ll x){return k*x+b;}
Line(ll kk=0,ll bb=0){
k=kk;b=bb;
}
};
struct Lichao_SegmentTree{
const ll LCinf=1e18;
#define ls ((u)<<1)
#define rs ((u)<<1|1)
ll crossX(Line i,Line j){
return (j.b-i.b)/(i.k-j.k);
}
struct node{
Line lin;
int l,r;
bool has_lin,vis;
}tr[4*N];
void build(int u,int l,int r){
tr[u].l=l;tr[u].r=r;
tr[u].vis=tr[u].has_lin=0;
if(l==r){
return;
}
else{
int mid=(l+r)>>1;
build(ls,l,mid);build(rs,mid+1,r);
}
return;
}
void insert(int u,int L,int R,Line x){
tr[u].vis=1;
if(tr[u].r<=R&&tr[u].l>=L){
if(!tr[u].has_lin){
tr[u].has_lin=1;
tr[u].lin=x;
return;
}
if(tr[u].lin.val(tr[u].l)>=x.val(tr[u].l)&&tr[u].lin.val(tr[u].r)>=x.val(tr[u].r)) return;
if(tr[u].lin.val(tr[u].l)<x.val(tr[u].l)&&tr[u].lin.val(tr[u].r)<x.val(tr[u].r)){tr[u].lin=x;return;}
int mid=(tr[u].l+tr[u].r)/2;
if(crossX(x,tr[u].lin)<=mid){
if(x.k<tr[u].lin.k) insert(ls,L,R,x);
else{insert(ls,L,R,tr[u].lin);tr[u].lin=x;}
}
else{
if(x.k>tr[u].lin.k) insert(rs,L,R,x);
else{insert(rs,L,R,tr[u].lin);tr[u].lin=x;}
}
return;
}
int mid=(tr[u].l+tr[u].r)/2;
if(R<=mid){insert(ls,L,R,x);}
else if(L>mid){insert(rs,L,R,x);}
else{insert(ls,L,R,x);insert(rs,L,R,x);}
}
ll query(int u,int x){
if(!tr[u].vis) return -LCinf;
ll ret;
if(!tr[u].has_lin){
ret=-LCinf;
}
else{
ret=tr[u].lin.val(x);
}
if(tr[u].l==tr[u].r) return ret;
int mid=(tr[u].l+tr[u].r)/2;
if(x<=mid) return max(ret,query(ls,x));
else return max(ret,query(rs,x));
}
}ST;
Splay
struct SplayTree{
struct Splay_Tree{
int son[2],fa,cnt,val,siz,tag;
}tree[N];
int root,cnt;
const int inf=2147483647;
void pushup(int u){
tree[u].siz=tree[tree[u].son[0]].siz+tree[tree[u].son[1]].siz+tree[u].cnt;
}
void pushdown(int x){
if(tree[x].tag){
}
}
int build(int l,int r,int fa){//根据数组 a 建树并返回根结点,如果不需要建树,请删除这一段代码
if(l>r) return 0;
int v=++cnt;
tree[v].fa=fa;
tree[v].cnt=1;
int mid=(l+r)>>1;
//tree[v].val=a[mid];
tree[v].son[0]=build(l,mid-1,v);
tree[v].son[1]=build(mid+1,r,v);
pushup(v);
return v;
}
bool check(int u){
return tree[tree[u].fa].son[1]==u;
}
void rotate(int u){//单次旋转操作
int fa=tree[u].fa;
int ffa=tree[fa].fa;
pushdown(fa);pushdown(u);
int k=check(u);
tree[ffa].son[check(fa)]=u;tree[u].fa=ffa;
tree[fa].son[k]=tree[u].son[k^1];tree[tree[u].son[k^1]].fa=fa;
tree[u].son[k^1]=fa;tree[fa].fa=u;
pushup(fa);pushup(u);
}
void splay(int u,int goal){//将 u 向上旋转直至父亲为 goal(goal=0->旋到根)
while(tree[u].fa!=goal){
int fa=tree[u].fa;
int ffa=tree[fa].fa;
pushdown(fa);pushdown(u);
if(ffa!=goal){
if(check(u)==check(fa)) rotate(fa);
else rotate(u);
}
rotate(u);
}
if(!goal) root=u;
}
void insert(int x){//插入一个数
int u=root,fa=0;
while(tree[u].val!=x&&u){
pushdown(u);
fa=u;
u=tree[u].son[x>tree[u].val];
}
if(u) tree[u].cnt++;
else{
u=++cnt;
if(fa) tree[fa].son[x>tree[fa].val]=u;
tree[u].fa=fa;tree[u].val=x;
tree[u].cnt=tree[u].siz=1;
}
splay(u,0);
}
void find(int x){//寻找一个数
int u=root;
while(x!=tree[u].val&&tree[u].son[x>tree[u].val]){
pushdown(u);
u=tree[u].son[x>tree[u].val];
}
splay(u,0);
}
void del(int x){//删除一个数
int l=frne(x,0);
int r=frne(x,1);
splay(l,0);splay(r,l);
int tmp=tree[r].son[0];
if(tree[tmp].cnt>1){
tree[tmp].cnt--;
splay(tmp,0);
}
else tree[r].son[0]=0;
}
int query(int rk){//查找排名为 rk 的数
int u=root;
pushdown(u);
while(1){
if(tree[tree[u].son[0]].siz>=rk){
u=tree[u].son[0];
}
else if(tree[tree[u].son[0]].siz+tree[u].cnt>=rk) return u;
else{
rk-=tree[tree[u].son[0]].siz+tree[u].cnt;
u=tree[u].son[1];
}
pushdown(u);
}
}
int frne(int x,int opt){//求 x 的前驱/后继
find(x);
int u=root;
if((!opt&&tree[u].val<x)||(opt&&tree[u].val>x)) return u;
pushdown(u);
u=tree[u].son[opt];
while(tree[u].son[opt^1]){
pushdown(u);
u=tree[u].son[opt^1];
}
return u;
}
}Splay;
//建议在操作开始前使用这两行代码来减少特判
//Splay.insert(-inf);Splay.insert(inf);
普通莫队
struct node{
int l,r,id,ans;
}q[N];
bool cmp1(node i,node j){
if(i.l/block==j.l/block) return i.r<j.r;
else return i.l/block<j.l/block;
}
bool cmp2(node i,node j){
return i.id<j.id;
}
void add(int k){
//do something
}
void del(int k){
//do something
}
void solve(){
scanf("%d%d",&n,&m);block=sqrt(n);
for(int i=1;i<=n;i++) scanf("%d",&c[i]);
for(int i=1;i<=m;i++){
scanf("%d%d",&q[i].l,&q[i].r);
q[i].id=i;
}
sort(q+1,q+1+m,cmp1);
int l=1,r=0;
for(int i=1;i<=m;i++){
while(r<q[i].r) add(++r);
while(r>q[i].r) del(r--);
while(l<q[i].l) del(l++);
while(l>q[i].l) add(--l);
//do something
}
sort(q+1,q+1+m,cmp2);
for(int i=1;i<=m;i++){
printf("%d\n",q[i].ans);
}
}
带修莫队
int cntq,cntr,block;
char op[5];
struct node{
int l,r,tim,id,ans;
}q[N];
struct node2{
int pos,col;
}R[N];
bool cmp(node i,node j){
if(i.l/block!=j.l/block) return i.l/block<j.l/block;
if(i.r/block!=j.r/block) return i.r/block<j.r/block;
return i.tim<j.tim;
}
bool cmp2(node i,node j){
return i.id<j.id;
}
void add(int k){
//do something
}
void del(int k){
//do something
}
void solve(){
scanf("%d%d",&n,&m);block=pow(n,2.0/3.0);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for(int i=1;i<=m;i++){
scanf("%s",op);
if(op[0]=='Q'){
cntq++;
scanf("%d%d",&q[cntq].l,&q[cntq].r);
q[cntq].id=cntq;q[cntq].tim=cntr;
}
else{
cntr++;
scanf("%d%d",&R[cntr].pos,&R[cntr].col);
}
}
sort(q+1,q+1+cntq,cmp);
int l=1,r=0,t=0;
for(int i=1;i<=cntq;i++){
while(r<q[i].r) add(++r);
while(r>q[i].r) del(r--);
while(l<q[i].l) del(l++);
while(l>q[i].l) add(--l);
while(t<q[i].tim){
t++;
if(R[t].pos>=q[i].l&&R[t].pos<=q[i].r) del(R[t].pos);
swap(a[R[t].pos],R[t].col);
if(R[t].pos>=q[i].l&&R[t].pos<=q[i].r) add(R[t].pos);
}
while(t>q[i].tim){
if(R[t].pos>=q[i].l&&R[t].pos<=q[i].r) del(R[t].pos);
swap(a[R[t].pos],R[t].col);
if(R[t].pos>=q[i].l&&R[t].pos<=q[i].r) add(R[t].pos);
t--;
}
q[i].ans=now;
}
sort(q+1,q+1+cntq,cmp2);
for(int i=1;i<=cntq;i++){
printf("%d\n",q[i].ans);
}
}
树上莫队
struct node{
int to,nxt;
}e[M];
int block,head[N],cnt,n,m,col[N];
void add(int u,int v){
e[++cnt].to=v;
e[cnt].nxt=head[u];
head[u]=cnt;
}
int euler[N],in[N],out[N],cnte;
int fa[N][20],dep[N];
void dfs(int u,int f){
euler[++cnte]=u;in[u]=cnte;
fa[u][0]=f;dep[u]=dep[f]+1;
for(int i=1;i<=19;i++){
fa[u][i]=fa[fa[u][i-1]][i-1];
}
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;if(v==f) continue;
dfs(v,u);
}
euler[++cnte]=u;out[u]=cnte;
}
int lca(int u,int v){
if(dep[u]<dep[v]) swap(u,v);
for(int i=19;i>=0;i--){
if(dep[fa[u][i]]>=dep[v]) u=fa[u][i];
}
if(u==v) return u;
for(int i=19;i>=0;i--){
if(fa[u][i]!=fa[v][i]) u=fa[u][i],v=fa[v][i];
}
return fa[u][0];
}
struct nodeModui{
int l,r,id,ans,ex;
}q[N];
bool cmp1(nodeModui i,nodeModui j){
if(i.l/block==j.l/block) return i.r<j.r;
else return i.l/block<j.l/block;
}
bool cmp2(nodeModui i,nodeModui j){
return i.id<j.id;
}
bool tag[N];
int tot[COL],now;
void work(int u){
tag[u]^=1;
if(tag[u]==1){
//do something
}
else{
//do something
}
}
void MoDui(){
sort(q+1,q+1+m,cmp1);
int l=1,r=0;
for(int i=1;i<=m;i++){
while(r<q[i].r) work(euler[++r]);
while(r>q[i].r) work(euler[r--]);
while(l<q[i].l) work(euler[l++]);
while(l>q[i].l) work(euler[--l]);
if(q[i].ex){
work(q[i].ex);
q[i].ans=now;
work(q[i].ex);
}
else{
q[i].ans=now;
}
}
}
void solve(){
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&col[i]);
for(int i=1,u,v;i<n;i++){
scanf("%d%d",&u,&v);
add(u,v);add(v,u);
}
dfs(1,1);block=sqrt(2*n);
scanf("%d",&m);
for(int i=1,u,v;i<=m;i++){
scanf("%d%d",&u,&v);
if(in[u]>in[v]) swap(u,v);
if(out[u]>=out[v]){
q[i].l=in[u];
q[i].r=in[v];
q[i].ex=0;
}
else{
q[i].l=out[u];
q[i].r=in[v];
q[i].ex=lca(u,v);
}
q[i].id=i;
}
MoDui();
sort(q+1,q+1+m,cmp2);
for(int i=1;i<=m;i++){
printf("%d\n",q[i].ans);
}
}
左偏树/可并堆
int fa[N],dis[N],ls[N],rs[N];
int find(int x){
return fa[x]==x?x:(fa[x]=find(fa[x]));
}
struct node{
int id,val;
}a[N];
bool operator <(node i,node j){
return i.val==j.val?i.id<j.id:i.val<j.val;
}
int merge(int x,int y){
if(!x||!y) return x+y;
if(a[y]<a[x]) swap(x,y);
rs[x]=merge(rs[x],y);
if(dis[rs[x]]>dis[ls[x]]) swap(rs[x],ls[x]);
dis[x]=dis[rs[x]]+1;
return x;
}
可持久化与分治类算法
可持久化线段树(主席树)
可持久化线段树通过维护多个版本的线段树来实现可持久化的效果。其核心是建立不同时间戳的多个根节点,但共用其中没有经过修改的部分。
可持久化字典树
可持久化字典树一般是 01 字典树,其中一个典型问题是:
- 给定 $n$ 个数 $a_1,a_2,\dots,a_n$。
- 每次询问一个区间 $[l,r]$ 和一个数 $x$,问 $a_l,a_{l+1},\dots,a_r$ 中与 $x$ 异或最大的数。
容易发现可持久化字典树和可持久化线段树没有本质区别,无非是两条边是 $0/1$ 而已。
CDQ 分治
cdq 分治是一种用于处理偏序关系的方法,可以通过在归并排序中更新答案的方式来处理掉问题中的一维偏序问题,通常搭配树状数组等其他数组结构使用。
有相当一部分有偏序关系的问题,或是能通过转换条件得到偏序关系的问题都可以使用 cdq 分治来帮助解决。特别的,由于归并排序是一个后序遍历,而 dp 类问题通常需要中序遍历,因此这种情况需要先通过归并排序处理出递归过程中的数组,再利用 cdq 分治进行处理。
整体二分
整体二分是将若干操作(修改,查询等)合在一起在值域上进行二分的操作,其函数的基本框架是 void GlobalDiv(int head,int tail,int l,int r),其中 $[head,tail]$ 为操作的范围,$[l,r]$ 为对应的值域。在整体二分中,我们每次 check 答案的范围在 $[l,mid]$ 还是 $[mid+1,r]$,然后根据修改操作和查询操作的答案范围,将这些操作分成两组,继续进行二分,直至 $lr$,则 $[head,tail]$ 中所有查询操作的答案均为 $l$。
整体二分通常仅在单次 check 的复杂度不低于 $O(n)$ 的时候使用。
- P2617 Dynamic Rankings
第二题的整体二分做法见我的题解 P4597 序列sequence 题解
代码
可持久化线段树(主席树)
struct SegmentTree{//可持久化线段树
int root[N<<1],tot;
struct node{
int l,r,sum,son[2],tag;
}tr[N<<5];
void pushup(int u){
// tr[u].sum=tr[tr[u].son[0]].sum+tr[tr[u].son[0]].tag*(tr[tr[u].son[0]].r-tr[tr[u].son[0]].l+1)
// +tr[tr[u].son[1]].sum+tr[tr[u].son[1]].tag*(tr[tr[u].son[1]].r-tr[tr[u].son[1]].l+1);
}
void build(int &u,int l,int r,int *A){
u=++tot;tr[u].l=l;tr[u].r=r;
if(l==r){
// tr[u].sum=A[l];
}
else{
int mid=(l+r)>>1;
build(tr[u].son[0],l,mid,A);
build(tr[u].son[1],mid+1,r,A);
pushup(u);
}
}
void add(int &u,int L,int R,int k){
//注意 u 会被改变,所以需要先 copy 一个 root 再 insert. 形如 ST.root[i]=ST.root[i-1];
tr[++tot]=tr[u];u=tot;//获得 copy 并修改原值
if(tr[u].r<=R&&tr[u].l>=L){
tr[u].tag+=k;//标记永久化,不下传
return;
}
int mid=(tr[u].l+tr[u].r)/2;
if(R<=mid){add(tr[u].son[0],L,R,k);}
else if(L>mid){add(tr[u].son[1],L,R,k);}
else{add(tr[u].son[0],L,R,k);add(tr[u].son[1],L,R,k);}
pushup(u);
}
ll query(int u,int L,int R,int tag){
if(tr[u].r<=R&&tr[u].l>=L) return tr[u].sum+(tag+tr[u].tag)*(tr[u].r-tr[u].l+1);
int mid=(tr[u].l+tr[u].r)/2;
if(R<=mid) return query(tr[u].son[0],L,R,tag+tr[u].tag);
else if(L>mid) return query(tr[u].son[1],L,R,tag+tr[u].tag);
else return query(tr[u].son[0],L,R,tag+tr[u].tag)+query(tr[u].son[1],L,R,tag+tr[u].tag);
}
}ST;
CDQ 分治
void cdq(int l,int r){
if(l==r) return;int mid=(l+r)>>1;
cdq(l,mid);cdq(mid+1,r);
int p1=l,pl=l,p2=mid+1;
while(p1<=mid&&p2<=r){
if(a[p1]<a[p2]){
t[pl++]=a[p1++];
//do something
}else{
t[pl++]=a[p2++];
//do something
}
}
while(p1<=mid){
t[pl++]=a[p1++];
//do something
}
while(p2<=r){
t[pl++]=a[p2++];
//do something
}
for(int i=l;i<=r;++i){
a[i]=t[i];
}
}
CDQ 分治 – DP 版本
void mergeSort(int l,int r,int deep){//先做 mergeSort
if(l==r){
t[l][deep].fi=a[l];
t[l][deep].se=l;
return;
}
int mid=(l+r)>>1;
mergeSort(l,mid,deep+1);
mergeSort(mid+1,r,deep+1);
int p1=l,pl=l,p2=mid+1;
while(p1<=mid&&p2<=r){
if(t[p1][deep+1].fi<t[p2][deep+1].fi){
t[pl++][deep]=t[p1++][deep+1];
}else{
t[pl++][deep]=t[p2++][deep+1];
}
}
while(p1<=mid){
t[pl++][deep]=t[p1++][deep+1];
}
while(p2<=r){
t[pl++][deep]=t[p2++][deep+1];
}
}
void cdq(int l,int r,int deep){//再做 CDQ
if(l==r){
//do something
return;
}
int mid=(l+r)>>1;
cdq(l,mid,deep+1);
int p1=l,p2=mid+1,premax=0;
while(p1<=mid&&p2<=r){
if(t[p1][deep+1].fi<t[p2][deep+1].fi)){
//do something
p1++;
}else{
//do something
p2++;
}
}
while(p2<=r){
//do something
p2++;
}
cdq(mid+1,r,deep+1);
}
整体二分
void GlobalDiv(int head,int tail,int l,int r){
if(head>tail) return;
if(l==r){
for(int i=head;i<=tail;i++){
//if(q[i].type==3) ans[q[i].id]=l;
//update answer
}
return;
}
int mid=(l+r)>>1;
for(int i=head;i<=tail;i++){
/*if(q[i].type==1&&q[i].val_r<=mid) add(q[i].pos_l,1);
else if(q[i].type==2&&q[i].val_r<=mid) add(q[i].pos_l,-1);
else if(q[i].type==3){
tmp[i]=query(q[i].val_r)-query(q[i].pos_l-1);
}//处理数据*/
}
/*for(int i=head;i<=tail;i++){
if(q[i].type==1&&q[i].val_r<=mid) add(q[i].pos_l,-1);
else if(q[i].type==2&&q[i].val_r<=mid) add(q[i].pos_l,1);
}//这一段是为了消除影响*/
int pl=0,pr=0;
for(int i=head;i<=tail;i++){
if(q[i].type==1||q[i].type==2){
/*if(q[i].val_r<=mid) tmpl[++pl]=q[i];
else tmpr[++pr]=q[i];//处理修改操作属于哪一部分*/
}
else {
/*if(tmp[i]>=q[i].k) tmpl[++pl]=q[i];
else{
q[i].k-=tmp[i];
tmpr[++pr]=q[i];
}//处理查询操作属于哪一部分*/
}
}
for(int i=head;i<head+pl;i++){
q[i]=tmpl[i-head+1];
}
for(int i=head+pl;i<=tail;i++){
q[i]=tmpr[i-head-pl+1];
}
GlobalDiv(head,head+pl-1,l,mid);
GlobalDiv(head+pl,tail,mid+1,r);
}
树上信息维护
树的 dfs 序
在二叉树中我们有前序,中序,后续。而对于一棵普通树,我们有三种常用的 dfs 序。
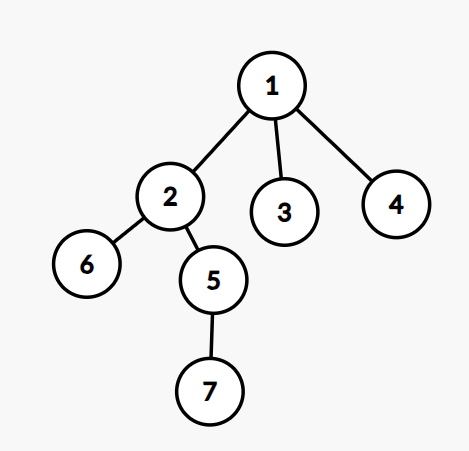
- dfs 序:第一次遍历一个点时把该点加入序列(上图的一个可能的 dfs 序为 1,4,2,5,7,6,3)。
- dfs 序通常用于子树和树链操作类问题。
- 扩展 dfs 序:第一次遍历一个点时,以及遍历一个点的儿子前,把该点加入序列(上图的一个可能的扩展 dfs 序为 1,1,4,1,2,2,5,5,7,2,6,1,3)。
- 对于两个点 $u,v$,其 LCA 就是 $[id_u,id_v]$ 区间中深度最低的点,容易发现这样的点一定是唯一的。可以通过维护一个 pair<depth,id> 来做到 $O(1)$ 查询 LCA。
- 通过扩展 dfs 序,我们可以把 LCA 问题转化为 RMQ 问题;通过笛卡尔树,我们可以把 RMQ 问题转化为 LCA 问题,这有时候有益于思考与解决。
- 欧拉序:在第一次遍历一个点和这个点遍历完成后,把该点加入序列(上图的一个可能的欧拉序为 1,4,4,2,5,7,7,5,6,6,2,3,3,1)。
- 欧拉序通常用于抵消前后的影响,例如树链上莫队,树链上亦或和。
- 也可以利用欧拉序列维护信息,例如ETT(欧拉环游树)。
注意,不论在哪一种序列,$id_x$ 都表示点 $x$ 第一次进入序列对应的时间戳($dfn$)。
树上差分与树上倍增
树上差分与一维差分类似。对于树链上的差分,通常在点 $u,v,lca(u,v),fa_{lca(u,v)}$ 四点处打 tag。
树上倍增的思想即倍增求 lca 的影响,不多赘述。
树链剖分/轻重链剖分
树链剖分的核心思想就是将树分解成若干条链,同一条的 dfs 序是连续的,并保证一个点可以经过不超过 $\log n$ 条不同的链到达树根。在轻重链剖分中,我们通过优先走重儿子(子树大小最大的儿子)来做到这一点。
完成链分解后,我们可以利用一些数据结构来维护。对于子树的操作,其等价于对一段 dfs 序连续的点进行操作;对于链的操作,其等价于对 $\log n$ 段 dfs 序连续的点进行操作。
例题:
树上启发式合并(dsu on tree)
我的学习笔记 树上启发式合并(dsu on tree)学习笔记
dsu on tree 与长链剖分部分参考四糸智乃的博客 长链剖分
dsu on tree 本身是一种比较简单的处理方式(类似莫队,是一种优雅的暴力),大致分为以下几步:
- 处理轻儿子,并消除影响。
- 处理重儿子。
- 把轻儿子的信息合并到重儿子/当前节点上。
- 统计答案。
dsu on tree 的时间复杂度是 $O(n\log n)$.
长链剖分
长链剖分实际上是 dsu on tree 的变种,在长链剖分中,轻重儿子以长链的最长长度来划分。长链剖分的步骤如下:
- 处理重儿子
- 处理轻儿子同时把轻儿子的信息往重儿子上边并
- 统计答案
在长链剖分中,答案通常以深度的形式的呈现,因此指定深度的询问问题才是长链剖分的用武之地。
Link-Cut Tree(动态树)
LCT 的底层原理是用 splay 维护动态的链分解。在 LCT 中,我们把一棵树分解为若干条链,而每条链都用 splay 进行维护。在一条被维护的链内,所有点的 key 即为其深度大小,在两条不同的链中,他们通过结构树相连,形如:
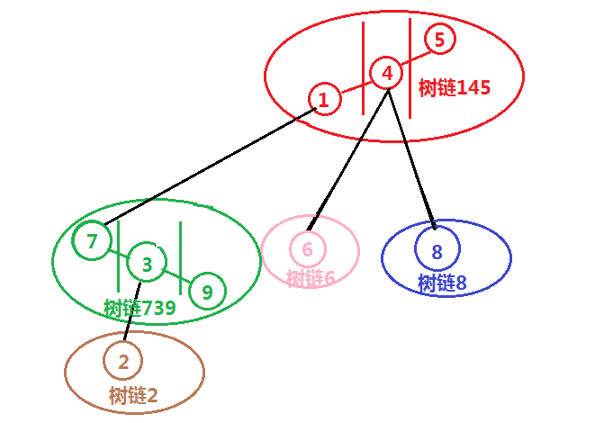
图源:四糸智乃老师的课件
在 LCT 中,有以下几种关键操作:
access(x)(将根节点到 $x$ 节点构造到同一条链中)make root(x)(将节点 $x$ 设置成整棵树的根)split(x,y)(将 $x,y$ 构造到同一条链中,且链的首尾为 $x ,y$)link(x,y)(将 $x,y$ 连接到 LCT 中)cut(x,y)(将 $x,y$ 从 LCT 中断开)lca(x,y,z)(查询以 $x$ 为根, $y$ 和 $z$ 的 lca)findroot(x)(查询 $x$ 节点所在树结构的树根是谁)
LCT 单次操作的时间复杂度是均摊 $O(\log n)$ 的。
树分治
树分治和序列上分治的思路整体类似,不过由于子树不止一个,通常需要使用容斥(或者一些其他的 trick 来进行处理),总体分为以下几步:
- 寻找当前树的重心
- 处理跨重心的树链。
- 收集并处理整棵树的信息
- 依次处理各个子树的信息
- 递归处理子树。
树分治的时间复杂度是 $O(n\log n)$。
点分树
点分治其实就是对于树分治问题的动态处理。
以下论述引用自四糸智乃老师的课件
点分树是典型的三层结构模型。
- 第一层是分治重心树,它是一个“区间树”它表示作用域的嵌套关系。
- 第二层是图论结构树,它表示第一层次中每一个节点的实际图论结构。
- 第三层是数据结构层,这里可以嵌套各种数据结构,包括数组、线段树、STL、平衡树。
前两层一般分别通过 fa_div(即分治过程中,分治中心树的父亲关系)和 belong(即每个结点在某一层属于哪个子树)两个数组表示,而第三层则是做题的关键。
虚树
虚树,就是对树中的关键结点及其 LCA 建树,而舍弃其他结点,以减少树的规模。
虚数的构建方法如下(修改自 phython96 的博客 虚树-树上动态规划的利器):
- 将根节点入栈,然后,依次尝试入栈所有关键结点。
- 若栈中只有一个元素,直接入栈。
- 否则,取即将入栈的元素 $u$ 和栈顶的 LCA。
- 若 LCA 即是栈顶,则直接将 $u$ 入栈。
- 否则,持续弹出栈顶的元素,并将新栈顶的点与被弹出的边连边,直至栈顶倒数第二个点的 $dfn$ 小于 LCA(即 $dfn[st[top-1]]<dfn[lca]$)。然后,根据 LCA 是否为当前栈顶的点决定是否要将 LCA 入栈,若要入栈,则先弹出栈顶,并将 LCA 与栈顶的点连边。
代码
树链剖分
int dep[N],son[N],siz[N],fa[N];
void dfs1(int u,int Fa){
dep[u]=dep[Fa]+1;siz[u]=1;fa[u]=Fa;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;if(v==Fa) continue;
dfs1(v,u);siz[u]+=siz[v];
if(!son[u]||siz[v]>siz[son[u]]) son[u]=v;
}
}
int top[N],dfn,id[N],idx[N];
void dfs2(int u,int Top){
top[u]=Top;id[u]=++dfn;idx[dfn]=u;
if(son[u]) dfs2(son[u],Top);
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;if(v==fa[u]||v==son[u]) continue;
dfs2(v,v);
}
}
int lca(int u,int v){
while(top[u]!=top[v]){
if(dep[top[u]]<dep[top[v]]) swap(u,v);
//do something
u=fa[top[u]];
}
return dep[u]<dep[v]?u:v;
}
Dsu on Tree
int son[N],siz[N],fa[N];
void dfs1(int u,int Fa){
siz[u]=1;fa[u]=Fa;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;if(v==Fa) continue;
dfs1(v,u);siz[u]+=siz[v];
if(!son[u]||siz[v]>siz[son[u]]) son[u]=v;
}
}
/*
int top[N],dfn,id[N],idx[N];
void dfs2(int u,int Top){
top[u]=Top;id[u]=++dfn;idx[dfn]=u;
if(son[u]) dfs2(son[u],Top);
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;if(v==fa[u]||v==son[u]) continue;
dfs2(v,v);
}
}//如果用不到其他数据结构,则 dfs2 非必需。
*/
void dfs(int u,int skp){
// BIT.add(a[u],1);
// 加入贡献
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;if(v==fa[u]||v==skp) continue;
dfs(v,skp);
}
}
void clean(int u){
// BIT.add(a[u],-1);
// 清除贡献
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;if(v==fa[u]) continue;
clean(v);
}
}
void dsu(int u){
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;if(v==son[u]||v==fa[u]) continue;
dsu(v);clean(v);
}
if(son[u]) dsu(son[u]);
dfs(u,son[u]);
// for(auto x:q[u]){
// ans[x.first]=BIT.query(x.second);
// }
// 统计答案
}
长链剖分
int son[N],len[N],fa[N];
void dfs1(int u,int Fa){
fa[u]=Fa;len[u]=1;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;if(v==Fa) continue;
dfs1(v,u);if(len[v]+1>len[u]) len[u]=len[v]+1;
if(!son[u]||len[v]>len[son[u]]) son[u]=v;
}
}
int dfn,L[N],R[N],idx[N];
void dfs2(int u){
L[u]=++dfn;R[u]=L[u]+len[u]-1;idx[dfn]=u;
if(son[u]) dfs2(son[u]);
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;if(v==fa[u]||v==son[u]) continue;
dfs2(v);
}
}
void dsu(int u){//长链剖分版本 dsu on tree
if(son[u]) dsu(son[u]);
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(v==fa[u]||v==son[u]) continue;
dsu(v);
for(int j=L[v],k=1;j<=R[v];j++,k++){
// ST.change(1,L[u]+k,ST.query(1,j,j));
// 将轻儿子的信息合并到重儿子上
}
}
// ST.change(1,L[u],(node2){a[idx[u]],a[idx[u]],a[idx[u]],0,0});
// 别忘了计入 u 点本身对 L[u] 的贡献
for(auto k:q[u]){
// node2 tmp=ST.query(1,L[u]+k.l,L[u]+k.r);
// ans[k.id].Max=tmp.Max;ans[k.id].Min=tmp.Min;ans[k.id].Sum=tmp.Sum;
//统计答案
}
}
LCT
struct LinkCutTree{
struct node{
int son[2],fa,cnt,val,siz,rev;
int sum;
}tr[N];
const int inf=2147483647;
void pushup(int u){
tr[u].siz=tr[tr[u].son[0]].siz+tr[tr[u].son[1]].siz+tr[u].cnt;
tr[u].sum=tr[tr[u].son[0]].sum^tr[tr[u].son[1]].sum^tr[u].val;
}
void reverse(int u){
swap(tr[u].son[0],tr[u].son[1]);
tr[u].rev^=1;
}
void pushdown(int u){
if(tr[u].rev){
if(tr[u].son[0]) reverse(tr[u].son[0]);
if(tr[u].son[1]) reverse(tr[u].son[1]);
tr[u].rev=0;
}
}
bool check(int u){
return tr[tr[u].fa].son[1]==u;
}
bool isRoot(int u){
return tr[u].fa == 0 || (tr[tr[u].fa].son[0] != u && tr[tr[u].fa].son[1] != u);
}
void rotate(int u){//单次旋转操作
int fa=tr[u].fa;
int ffa=tr[fa].fa;
int k=check(u);
if(!isRoot(fa)){tr[ffa].son[check(fa)]=u;}
tr[u].fa=ffa;
tr[fa].son[k]=tr[u].son[k^1];tr[tr[u].son[k^1]].fa=fa;
tr[u].son[k^1]=fa;tr[fa].fa=u;
pushup(fa);pushup(u);
}
int st[N];
void splay(int u){//将 u 向上旋转直至根结点
int v=u;st[st[0]=1]=v;
while(!isRoot(v)) st[++st[0]]=v=tr[v].fa;
while(st[0]) pushdown(st[st[0]--]);
while(!isRoot(u)){
int fa=tr[u].fa;
if(!isRoot(fa)){
if(check(u)==check(fa)) rotate(fa);
else rotate(u);
}
rotate(u);
}
}
int access(int u){
int tmp=0;
while(u){
splay(u);tr[u].son[1]=tmp;
pushup(u);
tmp=u;u=tr[u].fa;
}
return tmp;
}
int lca(int u,int v){
access(u);
return access(v);
}
int findRoot(int u){
access(u);
splay(u);
while(tr[u].son[0]){
u=tr[u].son[0];
pushdown(u);
}
splay(u);
return u;
}
void makeRoot(int u){
access(u);
splay(u);
reverse(u);
}
void link(int u,int v){
makeRoot(u);
if(findRoot(v) != u) tr[u].fa = v;
}
void split(int u,int v){
makeRoot(u);
access(v);
splay(v);
}
void cut(int u,int v){
split(u,v);
if(tr[v].son[0]==u){
tr[v].son[0]=tr[u].fa=0;
}
}
}LCT;
树分治
bool vis_div[N];
int gravity,totalsiz,msiz[N];
int get_gravity(int u,int fa){
int siz=1;msiz[u]=-1;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(v==fa||vis_div[v]) continue;
int tmp=get_gravity(v,u);
if(tmp>msiz[u]) msiz[u]=tmp;
siz+=tmp;
}
if(totalsiz-siz>msiz[u]) msiz[u]=totalsiz-siz;
if(gravity==-1||msiz[u]<msiz[gravity]) gravity=u;
return siz;
}
int get_size(int u,int fa){
int siz=1;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(v==fa||vis_div[v]) continue;
siz+=get_size(v,u);
}
return siz;
}
int ans[N],n,d;
//vector<int> dis[N];
void get_data(int x,int u,int fa,int dep){
/*if(dis[x].size()<=dep){
dis[x].push_back(1);
}
else dis[x][dep]++;*/
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;if(v==fa||vis_div[v]) continue;
get_data(x,v,u,dep+1);
}
}
void get_ans(int x,int y,int u,int fa,int dep){
/*if(d-dep<0) return;
if(d-dep<dis[x].size()&&d-dep<dis[y].size()) ans[u]+=dis[x][d-dep]-dis[y][d-dep];
else if(d-dep<dis[x].size()) ans[u]+=dis[x][d-dep]-dis[y][dis[y].size()-1];
else ans[u]+=dis[x][dis[x].size()-1]-dis[y][dis[y].size()-1];*/
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;if(v==fa||vis_div[v]) continue;
get_ans(x,y,v,u,dep+1);
}
}
void TreeDiv(int u){
totalsiz=get_size(u,u);
gravity=-1;
get_gravity(u,u);
u=gravity;vis_div[u]=1;
//while(!dis[u].empty()) dis[u].pop_back();
get_data(u,u,u,0);
/*for(int i=1;i<dis[u].size();i++){
dis[u][i]+=dis[u][i-1];
}
if(d<dis[u].size()) ans[u]+=dis[u][d];
else ans[u]+=dis[u][dis[u].size()-1];*/
//处理树中所有点对根节点的贡献。
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;if(vis_div[v]) continue;
//while(!dis[v].empty()) dis[v].pop_back();
//dis[v].push_back(0);
get_data(v,v,u,1);
/*for(int i=1;i<dis[v].size();i++){
dis[v][i]+=dis[v][i-1];
}*/
get_ans(u,v,v,u,1);
}
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;if(vis_div[v]) continue;
TreeDiv(v);
}
}
点分树
bool vis_div[N];
int gravity,totalsiz,msiz[N];
int get_gravity(int u,int fa){
int siz=1;msiz[u]=-1;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(v==fa||vis_div[v]) continue;
int tmp=get_gravity(v,u);
if(tmp>msiz[u]) msiz[u]=tmp;
siz+=tmp;
}
if(totalsiz-siz>msiz[u]) msiz[u]=totalsiz-siz;
if(gravity==-1||msiz[u]<msiz[gravity]) gravity=u;
return siz;
}
int get_size(int u,int fa){
int siz=1;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(v==fa||vis_div[v]) continue;
siz+=get_size(v,u);
}
return siz;
}
int n,m,dep_div[N];
int fa_div[N],belong[N][20];
int dis_to_gravity[N][20];
//vector<int> dis[N][20];
void get_data(int x,int u,int fa,int dep,int divdep){
/*if(dis[x][divdep].size()<=dep){
dis[x][divdep].push_back(1);
}
else dis[x][divdep][dep]++;*/
//维护需要的数据
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;if(v==fa||vis_div[v]) continue;
get_data(x,v,u,dep+1,divdep);
}
}
void get_belong(int x,int u,int fa,int divdep,int dist){
belong[u][divdep]=x;
dis_to_gravity[u][divdep]=dist;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;if(v==fa||vis_div[v]) continue;
get_belong(x,v,u,divdep,dist+1);
}
}
void TreeDiv(int u,int depth,int fa){
totalsiz=get_size(u,u);
gravity=-1;
get_gravity(u,u);
u=gravity;vis_div[u]=1;
fa_div[u]=fa;dep_div[u]=depth;
belong[u][depth]=u;
dis_to_gravity[u][depth]==0;
/*get_data(u,u,u,0,depth);
for(int i=1;i<dis[u][depth].size();i++){
dis[u][depth][i]+=dis[u][depth][i-1];
}*/
//维护需要的数据
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;if(vis_div[v]) continue;
//dis[v][depth].push_back(0);
get_belong(v,v,u,depth,1);
/*get_data(v,v,u,1,depth);
for(int i=1;i<dis[v][depth].size();i++){
dis[v][depth][i]+=dis[v][depth][i-1];
}*/
//维护需要的数据
}
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;if(vis_div[v]) continue;
TreeDiv(v,depth+1,u);
}
}
int get_ans(int u,int d){
int nowg=u,nowdp=dep_div[u];
int ans;
/*if(d<dis[u][nowdp].size()) ans=dis[u][nowdp][d];
else ans=dis[u][nowdp][dis[u][nowdp].size()-1];
nowg=fa_div[nowg];nowdp--;*/
//一边统计答案,一边进行修改,本模板恰巧没有修改而已
while(nowg){
int subfa=belong[u][nowdp];
/*int tmpd=d-dis_to_gravity[u][nowdp];
if(tmpd>=0){
if(tmpd<dis[nowg][nowdp].size()&&tmpd<dis[subfa][nowdp].size()){
ans+=dis[nowg][nowdp][tmpd]-dis[subfa][nowdp][tmpd];
}
else if(tmpd<dis[nowg][nowdp].size()){
ans+=dis[nowg][nowdp][tmpd]-dis[subfa][nowdp][dis[subfa][nowdp].size()-1];
}
else{
ans+=dis[nowg][nowdp][dis[nowg][nowdp].size()-1]-dis[subfa][nowdp][dis[subfa][nowdp].size()-1];
}
}*/
//一边统计答案,一边进行修改,本模板恰巧没有修改而已
nowg=fa_div[nowg];
nowdp--;
}
return ans;
}
虚树
int top,st[N],dfn[N];
void insert(int u){
if(top == 1) {st[++top] = u;return;}
int lca = LCA(u,st[top]);
if(lca == st[top]) {st[++top] = u;return ;}
while(top > 1 && dfn[lca] <= dfn[st[top-1]]){
add(st[top-1],st[top]);
--top;
}
if(lca != st[top]) {
add(lca,st[top]);
st[top] = lca;
}
st[++top] = u;
}
// 别忘了先 insert(1),即树根,不过也要注意不要重复 insert 树根。