题面

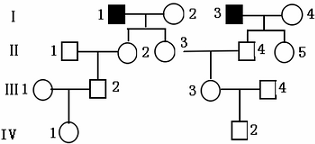
如图为某种常染色体隐性遗传病的系谱图（深色代表的个体是该遗传病患者，其余为表型正常的个体）。近亲结婚时，该遗传病发病率较高，假定图中第 Ⅳ 代的两个个体婚配生出一个患有该遗传病子代的概率是 $\frac{1}{48}$，那么，得出此概率值需要的限定条件是（　　）。

A．Ⅰ-2 和Ⅰ-4 必须是纯合子
B．Ⅱ-1、Ⅲ-1 和 Ⅲ-4 必须是纯合子
C．Ⅱ-2、Ⅱ-3、Ⅲ-2 和 Ⅲ-3 必须是杂合子
D．Ⅱ-4、Ⅱ-5、Ⅳ-1 和 Ⅳ-2 必须是杂合子

题目来源：温岭中学生物练习之综合练习（二）

答案

B

解析

由于 Ⅱ-2、Ⅱ-3、Ⅱ-4 不患病，而 Ⅰ-1、Ⅰ-3 为 $aa$，故 Ⅱ-2、Ⅱ-3、Ⅱ-4 一定为 $Aa$，A 项错误。

观察发现，$\frac{1}{48}=\frac{1}{4}\times\frac{1}{4}\times\frac{1}{3}$。首先发现 $Aa$ 和 $Aa$ 婚配生出有病子代的概率为 $\frac{1}{4}$。又发现 Ⅲ-3 有 $\frac{2}{3}$ 的概率为 $Aa$，考虑在 Ⅳ-2 中出现一个 $\frac{1}{3}$，而在 Ⅳ-1 中出现一个 $\frac{1}{4}$。故 Ⅲ-4 为 $AA$，这样 Ⅳ-2 为 $Aa$ 的概率为 $\frac{1}{3}$，同时 Ⅱ-1、Ⅲ-1 也均为 $AA$，这样 Ⅳ-1 为 $Aa$ 概率为 $\frac{1}{4}$，故子代患病概率为 $\frac{1}{3}\times \frac{1}{4}\times\frac{1}{4}=\frac{1}{48}$，发现 B 项符合题意。