本博客仅罗列定理,不给出证明,如需要请自行搜索。
质数相关
线性筛素数
inline void sieve(int n){//线性筛求 pri 和 phi
phi[1]=1;
for(int i=2;i<=n;i++){
if(!vis[i]){phi[i]=i-1;pri[++cnt]=i;}
for(int j=1;j<=cnt&&pri[j]*i<=n;j++){
vis[pri[j]*i]=1;
if(!(i%pri[j])){phi[i*pri[j]]=pri[j]*phi[i];break;}
else phi[i*pri[j]]=(pri[j]-1)*phi[i];
}
}
}
phi 为下文的欧拉函数,线性筛过程可以顺便求出,pri 即为素数(质数)数组。
算术基本定理
任何一个大于 $1$ 的正整数 $N$ 都能唯一分解为有限个质数的乘积,即:$N=p_1^{c_1}p_2^{c_2}\dots p_m^{c_m}$。
威尔逊定理
$p$ 是质数等价于 $(p-1)!\equiv-1\pmod p$。即两者互为充要条件。
欧几里得算法
朴素欧几里得
$\gcd(a,b)=\gcd(b,a\bmod b)$。
扩展欧几里得
求解 $ax+by=\gcd(a,b),\ a,b \in N$ 的一组整数解 $(x,y)$。
inline void exgcd(int a,int b){
if(!b){x=1,y=0;return;}
exgcd(b,a%b);
int t=x;x=y;y=t-(a/b)*y;
}
时间复杂度:$O(\log n)$。
应用:扩欧求逆元
求 $a\pmod{b}$ 意义下的逆元等价于求一个 $x$ 满足 $ax\equiv1\pmod{b}$,由于逆元存在,$a$ 与 $b$ 互质,故 $\gcd(a,b)=1$,所以即求 $ax+by=1=\gcd(a,b)$ 的解 $x$,显然可以用扩欧解决。
欧拉函数相关
欧拉函数
记 $\varphi(n)$ 为 $\le n$ 的正整数中与 $n$ 互质的数的个数(因此 $\varphi(1)=1$)。
通式:$\varphi(n)=n \prod\limits_{i=1}^{n}(1-\frac{1}{p_i})$,其中 $p_1,p_2\dots p_n$ 为 $n$ 的所有不重复的质因数。
容易发现,当 $p$ 为一个质数时,有 $\varphi(p)=p-1$。
欧拉定理
对于任意互素的 $a$ 和 $p$,有 $a^{\varphi(p)}\equiv 1\pmod{p}$。
推论:若 $a$ 和 $p$ 互素,则有 $a^b\equiv a^{b \operatorname{mod} \varphi(p)} \pmod{p}$。
扩展欧拉定理
费马小定理
若 $p$ 为素数且 $a$ 和 $p$ 互素,则有 $a^{p-1}\equiv 1\pmod{p}$。
应用:费马小定理求逆元
仅在模数为质数时适用。
若 $p$ 为质数,由 $a^{p-1}\equiv 1\pmod{p}$,故 $a \times a^{p-2}\equiv 1 \pmod{p}$,故 $a^{p-2}$ 即为 $a\pmod{p}$ 意义下的逆元,显然可以快速幂解决。
组合相关
卡特兰数
记 $f_n$ 为第 $n$ 项卡特兰数。
递推式:$f_1=1,f_n=f_{n-1}\frac{4n-2}{n+1}$。
通项式:$f_n=\frac{C_{2n}^n}{n+1}=C^n_{2n}-C^{n-1}_{2n}$。
卢卡斯定理
若 $p$ 为质数,有:
$C_n^m\equiv C_{n/p}^{m/p} C_{n\operatorname{mod} p}^{m\operatorname{mod} p} \pmod p$。(此处的 $/$ 为整除)。
二项式定理
$(x+y)^n=C_n^0x^ny^0+C_n^1x^{n-1}y^1+C_n^2x^{n-2}y^2+\dots+C_n^{n-1}x^1y^{n-1}+C_n^nx^0y^n$。
其他定理
裴蜀定理
对于 $ax+by=\gcd(a,b),\ a,b \in N$,一定存在一组整数 $x,y$ 使得该式成立。
扩展:对于 $a_1x_1+a_2x_2 \dots+a_nx_n=\gcd(a_1,a_2 \dots a_n),\ a_i\in N$,一定存在一组整数 $x_1,x_2\dots x_n$ 使得该式成立。
中国剩余定理
求解 $x$,满足方程组 $x ≡ a_i \pmod {m_i}$,其中 $m_i$ 两两互质。
令 $M = m_1m_2 … m_n, M_i = M/m_i$。
显然 $(M_i, m_i) = 1$,所以 $M_i$ 关于模 $m_i$ 的逆元存在。把这个逆元设为 $t_i$。
于是有:$M_it_i ≡ 1\pmod {m_i}, M_it_i ≡ 0\pmod {m_j}(j \ne i)$。
进一步:$a_iM_it_i ≡ a_i \pmod {m_i},a_iM_it_i ≡ 0 \pmod {m_j}(j \ne i)$。
因此解为 $x ≡ a_1M_1t_1 + a_2M_2t_2 + ⋯ + a_nM_nt_n \pmod M$,且在 $\bmod M$ 意义下是唯一解。
扩展中国剩余定理(同余方程式的合并)
合并两个同余方程:
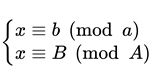
由已知式,可以令
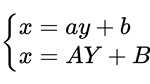
即 $ay+b=AY+B$,移项,得 $ay+A(-Y)=B-b$。
不妨直接将 $-Y$ 用 $Y$ 替换,即得到 $ay+AY=B-b$。
由扩展欧几里得可得到 $ay+AY=\gcd(a,A)$ 的一组解 $(y_0,Y_0)$,若 $B-b$ 不是 $\gcd(a,A)$ 的倍数,则原同余方程组无解。
否则,有 $a(y_0\times \frac{B-b}{\gcd(a,A)})+A(Y_0\times \frac{B-b}{\gcd(a,A)})=B-b$。
令 $t=y_0\times \frac{B-b}{\gcd(a,A)}$,则 $x=at+b$,可得到 $t$ 的最小正值 $t_0=t \bmod \frac{A}{\gcd(a,A)}$。
故原同余方程组可合并为 $x\equiv at_0+b\pmod{\operatorname{lcm}(a,A)}$。
注:若得到的 $t_0$ 为负,需要加上 $\frac{A}{\gcd(a,A)}$ 使其取到最小正值。
如有勘误,欢迎在评论区指出
评论