大概是要开一个文化课专题了，最近文化课有点崩，所以可能要抽点时间偶尔整理一些文化课的东西（基本都是错题）。

题面

设 $\vec{a},\vec{b},\vec{c}$ 为平面向量，$\vert \vec{a} \vert=\vert \vec{b} \vert=2,(2\vec{c}-\vec{a})\cdot(\vec{c}-\vec{b})=0$，则 $\vec{c}\cdot\vec{b}$ 的最大值为_____。

题目来源：浙江省温岭中学高一下第一次数学月考卷填空题最后一题。

答案

$\vec{c}\cdot\vec{b}$ 的最大值为 $\frac{17}{4}$。

解析

首先我们发现 $\vec{a},\vec{b}$ 长度已知而 $\vec{c}$ 长度未知，考虑将 $(2\vec{c}-\vec{a})\cdot(\vec{c}-\vec{b})=0$ 转化为 $\frac{1}{2}(\vec{c}-\frac{\vec{a}}{2})\cdot(\vec{c}-\vec{b})=0$，这样我们就可以作出下图：

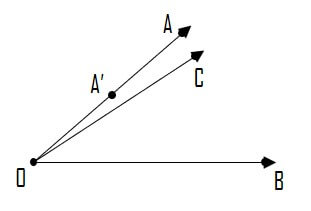
此图中，$\vec{a},\vec{b},\vec{c},\frac{\vec{a}}{2}$ 分别用 $\vec{OA},\vec{OB},\vec{OC},\vec{OA’}$ 表示。

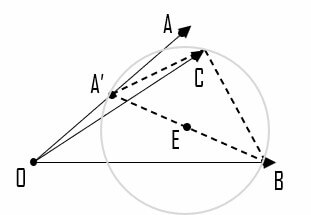
然后连接 $A’C,BC$，故有 $A’C\perp BC$，因此，点 $C$ 在一个以 $A’B$ 为直径的圆上，记圆心为点 $E$。

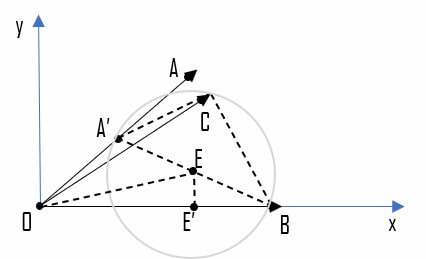
以 $OB$ 为 $x$ 轴正方向建立平面直角坐标系，则有 $B(2,0)$，设 $A'(\cos\theta,\sin\theta)$，则 $E(\frac{\cos\theta+2}{2},\frac{\sin\theta}{2})$。过点 $E$ 作 $x$ 轴的垂线交于点 $E’$，则 $OE’=\frac{\cos\theta+2}{2}$。

回到问题，我们需要求 $\vec{c}\cdot\vec{b}$ 的最大值，由于 $\vert \vec{b} \vert$ 是已知的，我们所需要的就是使 $\vec{c}$ 在 $\vec{b}$ 即在 $x$ 轴上的射影尽可能大。先假定 $A$ 的位置已经确定，则容易发现点 $C$ 在下图所示位置时射影取到最大：

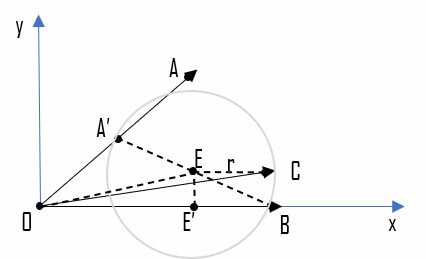
此时 $\vec{c}$ 在 $x$ 轴上的射影 $=OE’+r$。又有 $r=\frac{A’B}{2}=\frac{\sqrt{(\cos\theta-2)^2+\sin^2\theta}}{2}=\frac{\sqrt{5-4\cos\theta}}{2}$。

故 $\vec{c}\cdot\vec{b}=\vert \vec{b} \vert\times\vec{c}\ 在\ \vec{b}\ 上的射影=2(OE’+r)=\cos\theta+2+\sqrt{5-4\cos\theta}$。

设 $t=\sqrt{5-4\cos\theta}$，因为 $\cos\theta \in [-1,1]$，所以 $t\in[1,3]$。

故 $\vec{c}\cdot\vec{b}=-\frac{1}{4}t^2+t+\frac{13}{4}$，当 $t=2$ 时取到最大值 $\frac{17}{4}$。

故答案为 $\frac{17}{4}$。

碎碎念

水平还是太差劲了，这种简单的题目都写错了，希望能多多积累经验，文化课不要崩尤其是数学……