题意
题目链接。
有一张 $n\times\ n$ 的网格,有 $1,2,3$ 三种颜色,每轮交互库会给出一种颜色,你需要在剩余两种颜色中选一种颜色涂在一个格子上,不可以使任何两个相邻格子颜色相同。你需要扮演涂色者将所有格子涂上颜色。
解析
首先我们考虑到,如果有一个空格子,其上下左右四个格子中有两种颜色,你就输了(因为交互库可以一直给出剩余的这种颜色)。因此我们不能让这种情况发生,最好的解决办法就是尽可能只用两种颜色,且不相邻,将第三种颜色当作后手。
以这个思路,我们可以构造出一张理想网格。
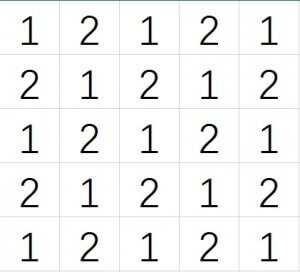
我们发现,在 $1$ 或 $2$ 全部被填完之前,不论交互库询问什么,我们都一定能在这个理想网格上填一格(例如,给出 $1$,就在应该填 $2$ 但尚未填的地方填一个 $2$)。
那当我们填完了其中一个数字时呢?我们发现我们已经无敌了,因为剩下的任意一个空格子,其上下左右四个格子都一定只有一种颜色,那么不论交互库给出哪一种颜色,我们都只需要填上另一种颜色,直至整张棋盘都被填满为止。
代码
#include<bits/stdc++.h>
using namespace std;
const int N=105;
int c[N][N];
int n,a,T,n1x,n1y,n2x,n2y;
int x,y;
bool fl;
int main(){
scanf("%d",&n);T=n*n;
n1x=n1y=1;
n2x=1,n2y=2;
x=y=1;
while(T--){
scanf("%d",&a);
if(!fl){//填理想网格
if(a==1){
c[n2x][n2y]=2;
printf("%d %d %d\n",2,n2x,n2y);
fflush(stdout);
n2y+=2;
if(n2y>n){
n2x+=1;
if(n2x%2==1) n2y=2;
else n2y=1;
}
if(n2x>n) fl=true;
}
else{
c[n1x][n1y]=1;
printf("%d %d %d\n",1,n1x,n1y);
fflush(stdout);
n1y+=2;
if(n1y>n){
n1x+=1;
if(n1x%2==1) n1y=1;
else n1y=2;
}
if(n1x>n) fl=true;
}
}
else{//有一个数字被填完了
while(x<=n&&y<=n){
if(!c[x][y]){
if(a==1){
if(c[x][y-1]==1||c[x][y+1]==1) c[x][y]=2;
else c[x][y]=3;
}
else if(a==2){
if(c[x][y-1]==1||c[x][y+1]==1) c[x][y]=3;
else c[x][y]=1;
}
else{
if(c[x][y-1]==1||c[x][y+1]==1) c[x][y]=2;
else c[x][y]=1;
}
printf("%d %d %d\n",c[x][y],x,y);
fflush(stdout);
y++;if(y>n){y=1;x++;}
break;
}
y++;if(y>n){y=1;x++;}
}
}
}
return 0;
}