博客参考:学委 的 博客 及 代码启示
暴力最大流
模板题:Luogu3376
在学习 Dinic 之前,必须先要知道暴力最大流的写法。
首先理解何为网络最大流。一张网络就是一张带权有向图,源点可以输出无限的流量,但是每一条边都有一个容量,需要满足这条边上的流量不能超出其容量(可以理解为输水系统),最后所有流量都会被汇点接收。我们需要求出这个网络运行时的总流量最大是多少,即网络最大流(可以理解是源点最多同时输出多少水可以正常流到汇点)。
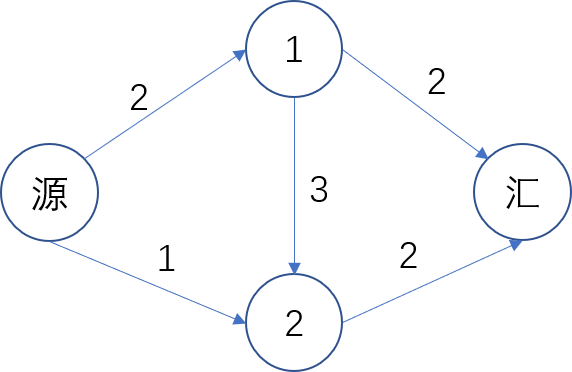
例如这张图,其最大流量就是 $3$(其中一种可行方案:分别走上面两条边和下面两条边,当然在该图中,也有其他方案可行)。
我们考虑计算机如何来解决这个问题。显然,我们可以爆搜可行路径。
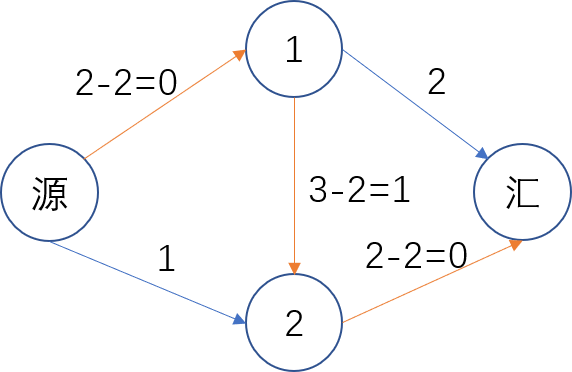
由于计算机不能纵观全图,因此在搜索时可能会搜索到这样一条路径,然后我们再从源点开始搜索时,发现下面那条流量为 $1$ 的边流不过去了(减完之后 $2$ 号点唯一可以走的边的容量只剩下 $1$ 了),因此此图中不存在可行路径了。这时的答案是 $2$,显然不是最优的。
朴素的爆搜中,这时候我们应该重新枚举方案,对于极小规模的图,这的确可行,但容易发现这种方案的复杂度在稍大的图中都是不可接受的。
我们考虑另一种方案。
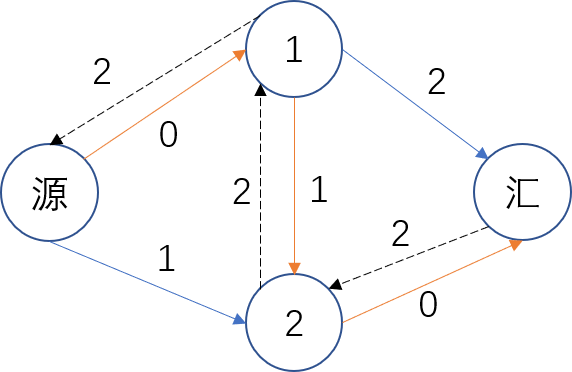
对于每一条我们走过的边,我们都建一条等同于流量的反边。这样我们尝试下面那条路时,就可以通过反边从 $2$ 走到 $1$,再走到汇点(相当于一个反悔操作)。容易发现这样就得到了一个最优解。
我们反复进行这样子的操作,由于每一次只要找到了汇点,总流量就一定能增加,因此该做法能够一直扩大总流量,直至没有任何一条线路可以走到汇点,此时跳出,我们当前的总流量就是最大流。
最后总结一下暴力最大流的做法:每次都 dfs 找有残量的路径(我们称为增广路),每次流过一条路时都填上等量的反边(反边可以提前建好),找到终点之后就结束本次 dfs,重新进行下一次 dfs,直至无法走到终点为止。
同时还有一个重要的性质,最小割=最大流。
何为最小割?割断任意条边,如果这些边被割断以后,源点与汇点不相连通,这些点就组成了一个割。而最小割就是所有割中,容量和最小的那个。
各种证明,参见 学委 的 博客,这里就跳过了。
但是我们发现暴力最大流的复杂度是非常不可靠的,因此,它无法通过该模板。
Dinic
模板题:Luogu3376
我们发现,在暴力最大流中,每一次 dfs 完都会跳出重来,这复杂度是很不可靠的,同时还可能在 dfs 过程中走很多远路,甚至在绕圈。那我们如何避免这种情况的发生呢?我们考虑两个优化:
- 对于点 $u$,向点 $v$ 输出流量之后,点 $v$ 最终会返回一个实际增广量。这时,如果 $u$ 仍有残量,我们不退出,而是尝试输出到其他边。
- 我们可以根据每一个点从源点出发之后的距离将图用 bfs 分层,$u$ 点在输出流量时只考虑输出给自己下一层的点,以防止过多的远路。
由于只要图中存在可行的增广路,bfs 与 dfs 一样也能够找到这条路,因此这样操作的正确性是能够得到保证的。
这次代码写了一点注释。
完整代码
Luogu3376 【模板】网络最大流
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e4+5;
int n,m,s,t,ans;
struct edge{
int to,nxt,w;
}e[N];
int head[N],cnt=1;//cnt=1 是为了改反边权值时方便
inline void add(int u,int v,int w){
e[++cnt].to=v;
e[cnt].w=w;
e[cnt].nxt=head[u];
head[u]=cnt;
}
int dep[N];
inline bool bfs(){//bfs 分层
for(int i=1;i<=n;i++) dep[i]=0;
queue<int> q;q.push(s);dep[s]=1;//由于下面直接写了 !dep[v],所以 dep[s] 初值为 1
while(!q.empty()){
int u=q.front();q.pop();
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(e[i].w&&(!dep[v])){
dep[v]=dep[u]+1;//标记距离
q.push(v);
}
}
}
if(dep[t]) return true;
return false;//走不到终点,返回 false
}
inline int dfs(int u,int in){
if(u==t) return in;
int out=0;
for(int i=head[u];i&∈i=e[i].nxt){
int v=e[i].to;
if(e[i].w&&dep[v]==dep[u]+1){//注意只能走到下一层
int tmp=dfs(v,min(in,e[i].w));
e[i].w-=tmp;e[i^1].w+=tmp;//反边同时加上流量
in-=tmp;
out+=tmp;//给予一次残量了之后继续尝试
}
}
if(!out) dep[u]=0;//这个点注定走不到终点,那就标记一下以后永远别走了
return out;
}
signed main(){
scanf("%lld%lld%lld%lld",&n,&m,&s,&t);
for(int i=1,u,v,w;i<=m;i++){
scanf("%lld%lld%lld",&u,&v,&w);
add(u,v,w);add(v,u,0);
}
while(bfs()){
ans+=dfs(s,1e18);//源点流量无穷大
}
printf("%lld\n",ans);
return 0;
}
几道经典/有趣题的建模
网络流的核心考点在于建模。
Luogu3386 【模板】二分图最大匹配
比较容易,建一个源点连向所有左部点,建一个汇点被所有右部点连向,然后对于每一条连接左部点和右部点的边,让这条边从左部点流向右部点即可。所有边的容量均为 $1$。
容易发现,我们将每两个可以匹配的点匹配在一起了之后(相当于连接他们两点的边有了流量),他们由源点流向/流向汇点的边的容量就没了,这样就保证了每一个点最多被匹配一次。建模完成之后,跑一遍最大流,所得结果就为最大匹配。
Luogu2065 [TJOI2011]卡片
这题写了题解。
题意:给定一个二分图,二分图上的每个点都有一个权值。如果一个左部点的权值和一个右部点的权值的 gcd 大于 1,则这两点之间有一条边。求二分图最大匹配。
只需要对于每一个点分解质因数,然后将这些因子作为中间点,再进行类似二分图最大匹配的操作就可以了。
Luogu2057 [SHOI2007]善意的投票 / [JLOI2010]冠军调查
题意:$n$ 个人有两种不同的意见并且有许多朋友,每个人都有初始意见。如果两个朋友之间意见不一致或是一个人的最终意见与初始意见不一致,就会产生冲突。让冲突数最小(详见题面)。
建超级源点连向所有意见为 $0$ 的,将所有意见为 $1$ 的连向超级汇点。对于每一对朋友,我们需要将两者连双向边。答案就为这张图的最小割。
为什么呢?如果图中存在一条路径从源点流向汇点,那么势必其路径中有一条边是由 $0$ 的点流向 $1$ 的点,这两点之间就仍有冲突。而我们可以通过割边来使这些冲突消失。
我们将割掉一条边表示以一个冲突为代价使这个限制消失。具体的,割掉源点流向 $0$ 点的边,就是这个 $0$ 点的最终意见不为 $0$,代价当然是冲突加一。割掉 $1$ 点流向汇点的边类似。割掉朋友之间的边就代表牺牲两者间朋友关系(正反边是不可能都被割去的)。
然后这个问题就被解决了。为什么要连双向边呢?因为两个朋友是平等的,你不知道这两个朋友之间的流向,所以需要建双向边。那么会不会双向边都被割掉而导致答案错误吗?由于在网络最大流中,最小割的割边一定是容量用尽的,但是由于两边不可能同时有流量(如果两边都有流量,不如两边流量同时减去那个容量小的,或者你也可以理解一个方向的容量用完了,由于需要添加反向边的容量,反向边的容量就会变大而不可能为 $0$),因此双向边不可能同时成为最小割的割边。
这样,这道题的建模就完成了!由于最大流=最小割,跑一边网络流即可。
Luogu2763 试题库问题
建一个超级源点,连向所有题目,容量为 $1$,然后所有题目都连向对应可行的类型,容量为 $1$,所有类型再连向超级汇点,容量为该类型需要的题数。跑一遍最大流,接着判断最大流是否为 $m$ ,若不是就不可行,可行再跑一遍图找出方案即可。
从上边几题中,我们容易认识到,建模在网络流问题中是最至关重要的。