题意

题目链接

给定 $n$ 个点，求一个由若干个点连接成的凸多边形，所包含的点数最多，输出点数。

解析

先说解法：将所有边按照 atan2(y,x) 的值排序， 然后枚举凸多边形起点，再遍历排序后的边进行 dp 转移，复杂度为 $O(n^3)$。

大致思路与已有题解相同，但是我在这里想要阐述一个困惑我许久的点：为什么是 atan2 ？

搜索百度百科可以发现，atan2 这个函数的返回值是方位角（而 atan 返回的仅是数字的反正切值），具体地：

然后我们来看一个凸多边形。

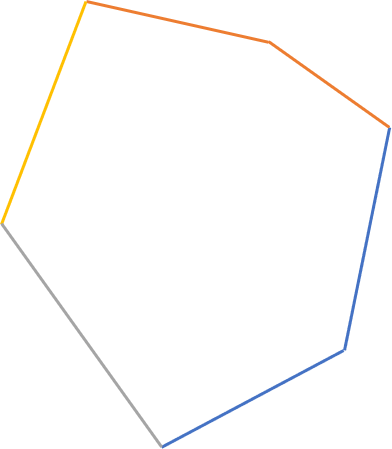
我们可以将这个凸多边形分为四部分，在图中分别用四种颜色表示。

对于蓝色部分：满足 $x,y>0$，返回值是一个在第一象限的值，记为 $k1$。

对于橙色部分：满足 $x<0,y>0$，返回值是一个在第二象限的值，记为 $k2$。

对于黄色部分：满足 $x,y<0$ 返回值是一个在第三象限的值，记为 $k3$。

对于灰色部分：满足 $x>0,y<0$ 返回值是一个在第四象限的值，记为 $k4$。

我们可以发现，$k3<k4<k1<k2$，同时对于每一个部分，容易发现其内部也是单调的（可以自行画图得出）。也就是说，如果我们找到了一个黄橙两个区域的交点作为起始点，那么接下来只要它所走的边的 atan2(y,x) 的值是单调递增的，最后回到这个点，形成的图形就一定是一个凸多边形。

因此，我们只需要枚举这个起始点，然后遍历排序好的边进行 dp，最后用这个起始点上的结果来更新答案就可以了，详见代码。

代码

#include<bits/stdc++.h>
using namespace std;
const int N=255;
int n,cnt,ans;
int f[N];
struct P{
    int u,v,x,y;
}a[N],e[N*N];
inline bool cmp(P i,P j){//按照 atan2 的值排序
    return atan2(i.y,i.x)<atan2(j.y,j.x);
}
int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
        scanf("%d%d",&a[i].x,&a[i].y);
    for(int i=1;i<=n;i++)//连边
        for(int j=1;j<=n;j++){
            if(i==j) continue;
            e[++cnt].u=i,e[cnt].v=j;
            e[cnt].x=a[j].x-a[i].x,e[cnt].y=a[j].y-a[i].y;
        }
    sort(e+1,e+1+cnt,cmp);
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++) f[j]=-1e9+7;
        f[i]=0;//枚举起始点
        for(int j=1;j<=cnt;j++)
            f[e[j].v]=max(f[e[j].v],f[e[j].u]+1);//动规
        ans=max(ans,f[i]);//更新答案
    }
    printf("%d\n",ans);
    return 0;
}